
【题目】如图,正方形![]() ,点
,点![]() 在边
在边![]() 上,且
上,且![]() ,
,![]() ,垂足为
,垂足为![]() ,且交
,且交![]() 于点
于点![]() ,
,![]() 与
与![]() 交于点
交于点![]() ,延长
,延长![]() 至
至![]() ,使
,使![]() ,连接
,连接![]() .有如下结论:①
.有如下结论:①![]() ;②
;②![]() ;③
;③![]() ;④
;④![]() .上述结论中,所有正确结论的序号是( )
.上述结论中,所有正确结论的序号是( )
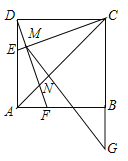
A. ①②B. ①③C. ①②③D. ②③④
 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案科目:初中数学 来源: 题型:
【题目】如图1,在△ABC中,AB=BC=5,AC=6.△ECD是△ABC沿BC方向平移得到的,连接AE.AC和BE相交于点O.
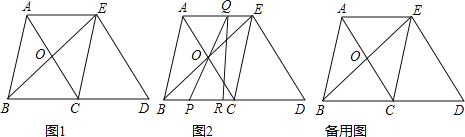
(1)判断四边形ABCE是怎样的四边形,说明理由;
(2)如图2,P是线段BC上一动点(图2),(不与点B、C重合),连接PO并延长交线段AE于点Q,QR⊥BD,垂足为点R.
①四边形PQED的面积是否随点P的运动而发生变化.若变化,请说明理由;若不变,求出四边形PQED的面积;
②当线段PB的长为何值时,△PQR与△BOC相似.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,以△ABC的边AB为直径的⊙O与边AC相交于点D,BC是⊙O的切线,E为BC的中点,连接BD、DE.
(1)求DE是⊙O的切线;
(2)设△CDE的面积为S1,四边形ABED的面积为S2,若S2=5S1,求tan∠BAC的值;
(3)在(2)的条件下,连接AE,若⊙O的半径为2,求AE的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
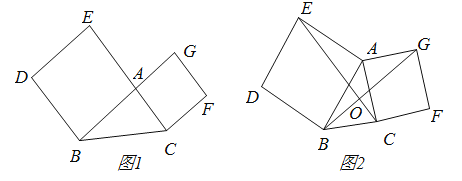
【题目】![]() 如图1,正方形
如图1,正方形![]() 和正方形,
和正方形,![]() 连接
连接![]() ,当
,当![]() 时,
时, ![]() 与
与![]() 的关系是?
的关系是?
![]() 如图2,将正方形
如图2,将正方形![]() 绕点
绕点![]() 顺时针旋转,
顺时针旋转,![]()
![]() 中结论是否仍然成立?若成立,请给出证明:若不成立,请说明理由;
中结论是否仍然成立?若成立,请给出证明:若不成立,请说明理由;
![]() 已知
已知![]() ,在旋转过程中,若直线
,在旋转过程中,若直线![]() 平分
平分![]() ,请画出相应的图形,并写出其中一种情形时
,请画出相应的图形,并写出其中一种情形时![]() 长的思路.
长的思路.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某旅行团32人在景区A游玩,他们由成人、少年和儿童组成.已知儿童10人,成人比少年多12人.
(1)求该旅行团中成人与少年分别是多少人?
(2)因时间充裕,该团准备让成人和少年(至少各1名)带领10名儿童去另一景区B游玩.景区B的门票价格为100元/张,成人全票,少年8折,儿童6折,一名成人可以免费携带一名儿童.
①若由成人8人和少年5人带队,则所需门票的总费用是多少元?
②若剩余经费只有1200元可用于购票,在不超额的前提下,最多可以安排成人和少年共多少人带队?求所有满足条件的方案,并指出哪种方案购票费用最少.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在□ABCD 中,对角线 AC 与 BD 相交于点 O ,点 E , F 分别为 OB , OD 的中点,延长 AE 至 G ,使 EG =AE ,连接 CG .
(1)求证: △ABE≌△CDF ;
(2)当 AB 与 AC 满足什么数量关系时,四边形 EGCF 是矩形?请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明将小球沿与地面成一定角度的方向击出,在不考虑空气阻力的条件下,小球的飞行高度y(m)与它的飞行时间x(s)满足二次函数关系,y与x的几组对应值如下表所示:
x(s) | 0 | 0.5 | 1 | 1.5 | 2 | … |
y(m) | 0 | 8.75 | 15 | 18.75 | 20 | … |
(Ⅰ)求y关于x的函数解析式(不要求写x的取值范围);
(Ⅱ)问:小球的飞行高度能否达到22m?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】北京世界园艺博览会(以下简称“世园会”)于2019年4月29日至10月7日在北京市延庆区举行.世园会为满足大家的游览需求,倾情打造了4条各具特色的游玩路线,如下表:
A | B | C | D |
漫步世园会 | 爱家乡,爱园艺 | 清新园艺之旅 | 车览之旅 |
小美和小红都计划去世园会游玩,她们各自在这4条路线中任意选择一条,每条线路被选择的可能性相同.
(1)求小美选择路线“清新园艺之旅”的概率是多少?
(2)用画树状图或列表的方法,求小美和小红恰好选择同一条路线的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com