
【题目】小明将小球沿与地面成一定角度的方向击出,在不考虑空气阻力的条件下,小球的飞行高度y(m)与它的飞行时间x(s)满足二次函数关系,y与x的几组对应值如下表所示:
x(s) | 0 | 0.5 | 1 | 1.5 | 2 | … |
y(m) | 0 | 8.75 | 15 | 18.75 | 20 | … |
(Ⅰ)求y关于x的函数解析式(不要求写x的取值范围);
(Ⅱ)问:小球的飞行高度能否达到22m?请说明理由.
【答案】(Ⅰ) y=﹣5x2+20x;(Ⅱ)小球的飞行高度不能达到22m,理由见解析.
【解析】
(Ⅰ)设y与x之间的函数关系式为y=ax2+bx(a≠0),然后再根据表格代入x=1时,y=15;x=2时,y=20可得关于a、b的方程组,再解即可得到a、b的值,进而可得函数解析式;
(Ⅱ)把函数解析式写成顶点式的形式可得小球飞行的最大高度,进而可得答案.
(Ⅰ)∵x=0时,y=0,
∴设y与x之间的函数关系式为y=ax2+bx(a≠0),
∵x=1时,y=15;x=2时,y=20,
∴![]() ,
,
解得![]() ,
,
∴y与x之间的函数关系式为y=﹣5x2+20x;
(Ⅱ)由(Ⅰ)得:y=﹣5x2+20x=﹣5(x﹣2)2+20,
∴小球飞行的最大高度为20m,
∵22>20,
∴小球的飞行高度不能达到22m.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】某高中学校为使高一新生入校后及时穿上合身的校服,现提前对某校九年级(1)班学生即将所穿校服型号情况进行摸底调查,并根据调查结果绘制如图两个不完整的统计图(校服型号以身高作为标准,共分为6种型号).
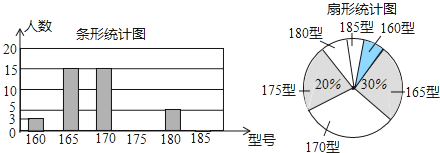
根据以上信息,解答下列问题:
(1)该班共有多少名学生?
(2)在条形统计图中,请把空缺部分补充完整;在扇形统计图中,请计算185型校服所对应的扇形圆心角的大小;
(3)求该班学生所穿校服型号的众数和中位数.如果该高中学校准备招收2000名高一新生,则估计需要准备多少套180型号的校服?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=ax2﹣9ax+18a的图象与x轴交于A,B两点(A在B的左侧),图象的顶点为C,直线AC交y轴于点D.
(1)连接BD,若∠BDO=∠CAB,求这个二次函数的表达式;
(2)是否存在以原点O为对称轴的矩形CDEF?若存在,求出这个二次函数的表达式,若不存在,请说明理由.
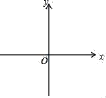
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形![]() ,点
,点![]() 在边
在边![]() 上,且
上,且![]() ,
,![]() ,垂足为
,垂足为![]() ,且交
,且交![]() 于点
于点![]() ,
,![]() 与
与![]() 交于点
交于点![]() ,延长
,延长![]() 至
至![]() ,使
,使![]() ,连接
,连接![]() .有如下结论:①
.有如下结论:①![]() ;②
;②![]() ;③
;③![]() ;④
;④![]() .上述结论中,所有正确结论的序号是( )
.上述结论中,所有正确结论的序号是( )
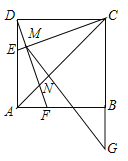
A. ①②B. ①③C. ①②③D. ②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知直线y=kx+b经过点A(0,2),B(﹣4,0)和抛物线y=x2.
(1)求直线的解析式;
(2)将抛物线y=x2沿着x轴向右平移,平移后的抛物线对称轴左侧部分与y轴交于点C,对称轴右侧部分抛物线与直线y=kx+b交于点D,连接CD,当CD∥x轴时,求平移后得到的抛物线的解析式;
(3)在(2)的条件下,平移后得到的抛物线的对称轴与x轴交于点E,P为该抛物线上一动点,过点P作抛物线对称轴的垂线,垂足为Q,是否存在这样的点P,使以点E,P,Q为顶点的三角形与△AOB相似?若存在,请求出点P的坐标;若不存在,请说明理由.
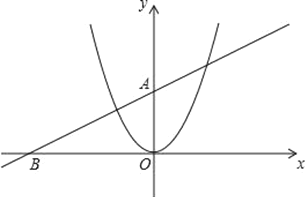
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示是一块含30°,60°,90°的直角三角板,直角顶点O位于坐标原点,斜边AB垂直于x轴,顶点A在函数y1=![]() (x>0)的图象上,顶点B在函数y2=
(x>0)的图象上,顶点B在函数y2= ![]() (x>0)的图象上,∠ABO=30°,则
(x>0)的图象上,∠ABO=30°,则![]() =( )
=( )
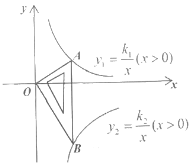
A.-3 B.3 C.![]() D.-
D.- ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】每年的3月15日是“国际消费者权益日”,许多家居商城都会利用这个契机进行打折促销活动.甲卖家的A商品成本为600元,在标价1000元的基础上打8折销售.
(1)现在甲卖家欲继续降价吸引买主,问最多降价多少元,才能使利润率不低于20%?
(2)据媒体爆料,有一些卖家先提高商品价格后再降价促销,存在欺诈行为.乙卖家也销售A商品,其成本、标价与甲卖家一致,以前每周可售出50件,现乙卖家先将标价提高2m%,再大幅降价24m元,使得A商品在3月15日那一天卖出的数量就比原来一周卖出的数量增加了 ![]() m%,这样一天的利润达到了20000元,求m的值.
m%,这样一天的利润达到了20000元,求m的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是由7个同样大小的正方体摆成的几何体.将正方体①移走后,所得几何体( )
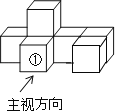
A. 主视图不变,左视图不变
B. 左视图改变,俯视图改变
C. 主视图改变,俯视图改变
D. 俯视图不变,左视图改变
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校为了更好地让学生适应中考体育:“1分钟跳绳”项目,对全校九年级200名学生进行了“1分钟跳绳”的测试,现随机抽取20名学生成绩进行分析,过程如下:
收集数据 20名学生的“1分钟跳绳”成绩(单位:个)如下
110 125 134 135 115 146 148 124 153 145
157 160 162 162 165 168 172 128 137 130
整理数据 请你按如下表格分组整理、描述样本数据,并把下列表格补充完整.(说明:每分钟跳绳个数达到160个及以上得满分)
成绩 |
|
|
|
|
|
等级 |
|
|
|
|
|
人数 |
成绩 |
|
|
等级 |
|
|
人数 |
分析数据 请将下列表格补充完整:
平均数 | 中位数 | 满分率 |
143.8 | 30% |
得出结论
(1)用样本中的统计量估计全校九年级学生“1分钟跳绳”等级为__________;
(2)估计该校九年级200名学生中测试“1分钟跳绳”等级为![]() 的人数.
的人数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com