
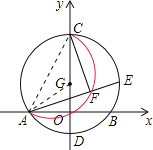
【题目】如图,以G(0,1)为圆心,半径为2的圆与x轴交于A、B两点,与y轴交于C、D两点,点E为⊙G上一动点,CF⊥AE于F.当点E从点B出发顺时针运动到点D时,点F所经过的路径长为( )

A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
【答案】B
【解析】分析:连接AC,AG,由OG垂直于AB,利用垂径定理得到O为AB的中点,由G的坐标确定出OG的长,在直角三角形AOG中,由AG与OG的长,利用勾股定理求出AO的长,进而确定出AB的长,由CG+GO求出OC的长,在直角三角形AOC中,利用勾股定理求出AC的长,由CF垂直于AE,得到三角形ACF始终为直角三角形,点F的运动轨迹为以AC为直径的半径,如图中红线所示,当E位于点B时,CO⊥AE,此时F与O重合;当E位于D时,CA⊥AE,此时F与A重合,可得出当点E从点B出发顺时针运动到点D时,点F所经过的路径长![]() ,在直角三角形ACO中,利用锐角三角函数定义求出∠ACO的度数,进而确定出
,在直角三角形ACO中,利用锐角三角函数定义求出∠ACO的度数,进而确定出![]() 所对圆心角的度数,再由AC的长求出半径,利用弧长公式即可求出
所对圆心角的度数,再由AC的长求出半径,利用弧长公式即可求出![]() 的长.
的长.
详解:连接AC,AG,
∵GO⊥AB,
∴O为AB的中点,即AO=BO=![]() AB,
AB,
∵G(0,1),即OG=1,
∴在Rt△AOG中,根据勾股定理得:AO=![]() ,
,
∴AB=2AO=2![]() ,
,
又CO=CG+GO=2+1=3,
∴在Rt△AOC中,根据勾股定理得:AC=![]() ,
,
∵CF⊥AE,
∴△ACF始终是直角三角形,点F的运动轨迹为以AC为直径的半圆,
当E位于点B时,CO⊥AE,此时F与O重合;当E位于D时,CA⊥AE,此时F与A重合,
∴当点E从点B出发顺时针运动到点D时,点F所经过的路径长![]() ,
,
在Rt△ACO中,tan∠ACO=![]() ,
,
∴∠ACO=30°,
∴![]() 度数为60°,
度数为60°,
∵直径AC=2![]() ,
,
∴![]() 的长为
的长为![]() ,
,
则当点E从点B出发顺时针运动到点D时,点F所经过的路径长![]() .
.
故选B.


 课前课后同步练习系列答案
课前课后同步练习系列答案 课堂小作业系列答案
课堂小作业系列答案 黄冈小状元口算速算练习册系列答案
黄冈小状元口算速算练习册系列答案 成功训练计划系列答案
成功训练计划系列答案 倍速训练法直通中考考点系列答案
倍速训练法直通中考考点系列答案科目:初中数学 来源: 题型:
【题目】如图,四边形OABC是平行四边形,以O为圆心,OA为半径的圆交AB于D,延长AO交⊙O于E,连接CD,CE,若CE是⊙O的切线,解答下列问题:
(1)求证:CD是⊙O的切线;
(2)若BC=3,CD=4,求平行四边形OABC的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
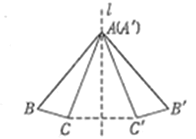
【题目】如图,△ABC和△A'B'C'关于直线l对称,下列结论:①△ABC≌△A'B'C' ;②∠BAC=∠B'A'C';③直线l不一定垂直平分线段CC';④直线BC与B'C'的交点一定在直线l上.其中正确的是________ (填序号).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】矩形纸片ABCD中,AB=10,AD=8,将纸片折叠,使点B落在CD上的B′处,折痕为AE,在折痕AE上存在一点P到边CD的距离与到点B的距离相等,则此相等的距离为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,抛物线![]() 与
与![]() 轴交于点
轴交于点![]() ,
,![]() ,与
,与![]() 轴交于点
轴交于点![]() ,直线
,直线![]() 经过
经过![]() ,
,![]() 两点.
两点.
![]() 求抛物线的解析式;
求抛物线的解析式;
![]() 在
在![]() 上方的抛物线上有一动点
上方的抛物线上有一动点![]() .
.
①如图![]() ,当点
,当点![]() 运动到某位置时,以
运动到某位置时,以![]() ,
,![]() 为邻边的平行四边形第四个顶点恰好也在抛物线上,求出此时点
为邻边的平行四边形第四个顶点恰好也在抛物线上,求出此时点![]() 的坐标;
的坐标;
②如图![]() ,过点
,过点![]() ,
,![]() 的直线
的直线![]() 交
交![]() 于点
于点![]() ,若
,若![]() ,求
,求![]() 的值.
的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2002年在北京召开的世界数学大会会标图案是由四个全等的直角三角形围成的一个大正方形,中间的阴影部分是一个小正方形的“赵爽弦图”.若这四个全等的直角三角形有一个角为30°,顶点B1、B2、B3、…、Bn和C1、C2、C3、…、Cn分别在直线![]() 和x轴上,则第n个阴影正方形的面积为
和x轴上,则第n个阴影正方形的面积为 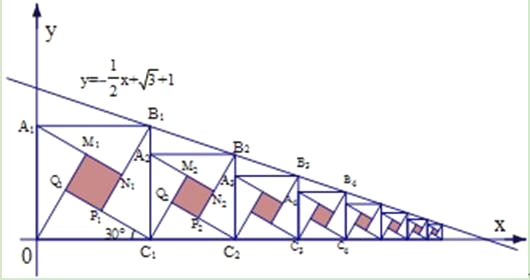
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知直线![]() 与双曲线
与双曲线![]() (k>0)交于A、B两点,点B的坐标为(﹣4,﹣2),C为双曲线
(k>0)交于A、B两点,点B的坐标为(﹣4,﹣2),C为双曲线![]() (k>0)上一点,且在第一象限内,若△AOC的面积为6.
(k>0)上一点,且在第一象限内,若△AOC的面积为6.
(1)求双曲线的解析式;
(2)求点C的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,△ABC的位置如图所示.
(1)顶点A关于x轴对称的点A′的坐标(____________),顶点B的坐标(____________),顶点C关于原点对称的点C′的坐标(____________).
(2)△ABC的面积为_____.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com