
分析 (1)根据方程的系数结合根的判别式即可得出△=m2+96>0,由此即可证出不论m为何值,方程总有两个不相等的实数根;
(2)设方程的另一根为n,将x=$\frac{2}{3}$代入原方程求出m的值,再由根与系数的关系可得出$\frac{2}{3}$n=-$\frac{8}{3}$,解之即可得出方程的另一个根.
解答 (1)证明:∵在方程3x2+mx-8=0中,△=m2-4×3×(-8)=m2+96>0,
∴不论m为何值,方程总有两个不相等的实数根;
(2)解:设方程的另一根为n,
将x=$\frac{2}{3}$代入原方程得:3×$(\frac{2}{3})^{2}$+$\frac{2}{3}$m-8=0,
解得:m=10,
由根与系数的关系可知:$\frac{2}{3}$n=-$\frac{8}{3}$,
∴n=-4.
答:方程另一个根为-4,m的值为10.
点评 本题考查了根的判别式、一元二次方程的解以及根与系数的关系,解题的关键是:(1)找出根的判别式△=m2+96>0;(2)将x=$\frac{2}{3}$代入原方程求出m的值.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
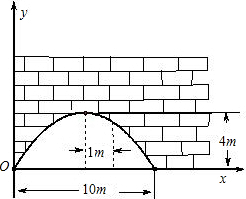 有一个抛物线形的拱形桥洞,桥洞离水面的最大高度为 4m,跨度为 10m,如图所示,把它的图形放在直角坐标系中.
有一个抛物线形的拱形桥洞,桥洞离水面的最大高度为 4m,跨度为 10m,如图所示,把它的图形放在直角坐标系中.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 (1)如图,在方格纸中先通过向上平移4个单位长,由图形A得到图形B,再由图形B先向右平移4个单位长度(怎样平移),再绕点P2顺时针旋转90°(怎样旋转)得到图形C(对于平移变换要求回答出平移的方向和平移的距离;对于旋转变换要求回答出旋转中心、旋转方向和旋转角度);
(1)如图,在方格纸中先通过向上平移4个单位长,由图形A得到图形B,再由图形B先向右平移4个单位长度(怎样平移),再绕点P2顺时针旋转90°(怎样旋转)得到图形C(对于平移变换要求回答出平移的方向和平移的距离;对于旋转变换要求回答出旋转中心、旋转方向和旋转角度);查看答案和解析>>
科目:初中数学 来源: 题型:选择题
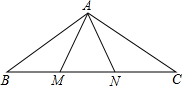 如图,△ABN≌△ACM,AB=AC,BN=CM,∠B=50°,∠ANB=60°,则∠MAC的度数等于( )
如图,△ABN≌△ACM,AB=AC,BN=CM,∠B=50°,∠ANB=60°,则∠MAC的度数等于( )| A. | 120° | B. | 70° | C. | 60° | D. | 50°. |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
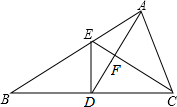 △ABC中,D是BC的中点,且AD=AC,DE⊥BC,与AB相交于点E,EC与AD相交于点F.
△ABC中,D是BC的中点,且AD=AC,DE⊥BC,与AB相交于点E,EC与AD相交于点F.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com