
 学校数学社团的同学们在学生中开展“了解校训意义”的调查活动.采取随机抽样的方式进行问卷调查.问卷调查的结果分为A、B、C、D四类.A类表示非常了解;B类表示比较了解;C类表示基本了解;D类表示不太了解.(要求每位同学必须选并且只能选择一项)统计数据整理如表:
学校数学社团的同学们在学生中开展“了解校训意义”的调查活动.采取随机抽样的方式进行问卷调查.问卷调查的结果分为A、B、C、D四类.A类表示非常了解;B类表示比较了解;C类表示基本了解;D类表示不太了解.(要求每位同学必须选并且只能选择一项)统计数据整理如表:| 类别 | A | B | C | D |
| 频数 | 20 | m | 11 | 4 |
| 频率 | n | 0.3 | 0.22 | 0.08 |
分析 (1)首先求出总人数,进而可求出m和n的值;
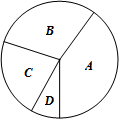
(2)由B所占的频率即可求出B类同学数所对应的圆心角的度数;
(3)画树状图或列表得出所有等可能的情况数,找出恰好是甲与乙的情况,即可确定出所求概率.
解答 解:
(1)由统计表可知总人数=11÷0.22=50人,所以m=50×0.3=15,n=20÷50=0.4,
故答案为:15;0.4;
(2)B类同学数所对应的圆心角的度数=0.3×360°=108°;
(3)由题意列表得
| ①\② | 甲 | 乙 | 丙 | 丁 |
| 甲 | 甲乙 | 甲丙 | 甲丁 | |
| 乙 | 乙甲 | 乙丙 | 乙丁 | |
| 丙 | 丙甲 | 丙乙 | 丙丁 | |
| 丁 | 丁甲 | 丁乙 | 丁丙 |
点评 此题考查的是用列表法或树状图法求概率以及扇形统计图和统计表的有关知识.列表法可以不重复不遗漏的列出所有可能的结果,适合于两步完成的事件;树状图法适合两步或两步以上完成的事件;解题时要注意此题是放回实验还是不放回实验.用到的知识点为:概率=所求情况数与总情况数之比.


科目:初中数学 来源: 题型:选择题
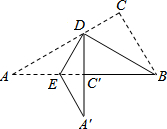 如图的实线部分是由Rt△ABC经过两次折叠得到的,首先将Rt△ABC沿BD折叠,使点C落在斜边上的点C′处,再沿DE折叠使点A落在DC′延长线上的点A′处,若图中,∠A=30°,BC=5cm,则折痕DE的长为( )
如图的实线部分是由Rt△ABC经过两次折叠得到的,首先将Rt△ABC沿BD折叠,使点C落在斜边上的点C′处,再沿DE折叠使点A落在DC′延长线上的点A′处,若图中,∠A=30°,BC=5cm,则折痕DE的长为( )| A. | $\sqrt{3}$ | B. | 2$\sqrt{3}$ | C. | 2$\sqrt{5}$ | D. | $\frac{10}{3}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
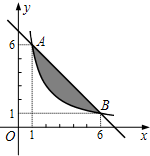 如果一个点的横、纵坐标均为整数,那么我们称这个点是格点,如图,A、B两点在函数y=$\frac{k}{x}$(x>0)的图象上,则图中阴影部分(不包括边界)所含格点的个数为3个.
如果一个点的横、纵坐标均为整数,那么我们称这个点是格点,如图,A、B两点在函数y=$\frac{k}{x}$(x>0)的图象上,则图中阴影部分(不包括边界)所含格点的个数为3个.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
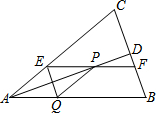 如图,等腰三角形ABC中,AB=AC,AD平分∠BAC交BC于点D,在线段AD上任取一点P(点A除外),过点P作EF∥AB,分别交AC,BC于点E和点F,作PQ∥AC,交
如图,等腰三角形ABC中,AB=AC,AD平分∠BAC交BC于点D,在线段AD上任取一点P(点A除外),过点P作EF∥AB,分别交AC,BC于点E和点F,作PQ∥AC,交查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 菱形ABCD的边长为3m,∠A=60°,弧CD是以点B为圆心,BC长为半径的弧,弧BD是以A为圆心,AB长为半径的弧,则阴影部分面积为$\frac{9}{4}$$\sqrt{3}$m2(结果保留根号).
菱形ABCD的边长为3m,∠A=60°,弧CD是以点B为圆心,BC长为半径的弧,弧BD是以A为圆心,AB长为半径的弧,则阴影部分面积为$\frac{9}{4}$$\sqrt{3}$m2(结果保留根号).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com