
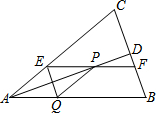
 如图,等腰三角形ABC中,AB=AC,AD平分∠BAC交BC于点D,在线段AD上任取一点P(点A除外),过点P作EF∥AB,分别交AC,BC于点E和点F,作PQ∥AC,交
如图,等腰三角形ABC中,AB=AC,AD平分∠BAC交BC于点D,在线段AD上任取一点P(点A除外),过点P作EF∥AB,分别交AC,BC于点E和点F,作PQ∥AC,交分析 (1)先证出四边形AEPQ为平行四边形,关键是找一组邻边相等,由AD平分∠BAC和PE∥AQ可证∠EAP=∠EPA,得出AE=EP,即可得出结论;
(2)S菱形AEPQ=EP•h,S平行四边形EFBQ=EF•h,若菱形AEPQ的面积为四边形EFBQ面积的一半,则EP=$\frac{1}{2}$EF,因此P为EF中点时,S菱形AEPQ=$\frac{1}{2}$S四边形EFBQ.
解答 (1)证明:∵EF∥AB,PQ∥AC,
∴四边形AEPQ为平行四边形,
∴∠BAD=∠EPA,
∵AB=AC,AD平分∠CAB,
∴∠CAD=∠BAD,
∴∠CAD=∠EPA,
∴EA=EP,
∴四边形AEPQ为菱形.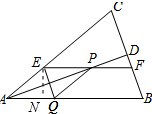
(2)解:P为EF中点,即AP=$\frac{2}{3}$AD时,S菱形AEPQ=$\frac{1}{2}$S四边形EFBQ
∵四边形AEPQ为菱形,
∴AD⊥EQ,
∵AB=AC,AD平分∠BAC,
∴AD⊥BC,
∴EQ∥BC,
又∵EF∥AB,
∴四边形EFBQ为平行四边形.
作EN⊥AB于N,如图所示:
则S菱形AEPQ=EP•EN=$\frac{1}{2}$EF•EN=$\frac{1}{2}$S四边形EFBQ.
点评 此题主要考查了菱形的判定与性质、平行四边形的判定与性质、等腰三角形的判定与性质;熟练掌握等腰三角形的性质,证明四边形是平行四边形是解决问题的关键.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:选择题
| A. | 1+(1-x)=1 | B. | 1-(1-x)=1 | C. | 1+(1-x)=x-3 | D. | 1-(1-x)=x-3 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
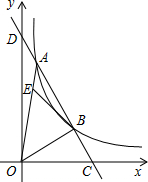 如图,一次函数与反比例函数y=$\frac{k}{x}$(x>0)的图象在第一象限交于A、B两点,交x轴于点C,交y轴于点D,且$\frac{CB}{BA}$=$\frac{1}{2}$.点E在线段OA上一点,OE=3EA,若△AEB的面积为S,则S与k之间的关系满足( )
如图,一次函数与反比例函数y=$\frac{k}{x}$(x>0)的图象在第一象限交于A、B两点,交x轴于点C,交y轴于点D,且$\frac{CB}{BA}$=$\frac{1}{2}$.点E在线段OA上一点,OE=3EA,若△AEB的面积为S,则S与k之间的关系满足( )| A. | k=$\frac{7}{2}$S | B. | k=3S | C. | k=$\frac{8}{3}$S | D. | k=$\frac{5}{2}$S |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
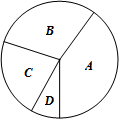 学校数学社团的同学们在学生中开展“了解校训意义”的调查活动.采取随机抽样的方式进行问卷调查.问卷调查的结果分为A、B、C、D四类.A类表示非常了解;B类表示比较了解;C类表示基本了解;D类表示不太了解.(要求每位同学必须选并且只能选择一项)统计数据整理如表:
学校数学社团的同学们在学生中开展“了解校训意义”的调查活动.采取随机抽样的方式进行问卷调查.问卷调查的结果分为A、B、C、D四类.A类表示非常了解;B类表示比较了解;C类表示基本了解;D类表示不太了解.(要求每位同学必须选并且只能选择一项)统计数据整理如表:| 类别 | A | B | C | D |
| 频数 | 20 | m | 11 | 4 |
| 频率 | n | 0.3 | 0.22 | 0.08 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
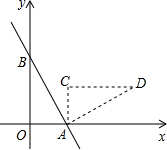 如图,一次函数y=-$\frac{4}{3}$x+4的图象与x轴、y轴分别交于A、B两点,把△AOB绕点A顺时针旋转90°后得到△ACD,则点D的坐标是(7,3).
如图,一次函数y=-$\frac{4}{3}$x+4的图象与x轴、y轴分别交于A、B两点,把△AOB绕点A顺时针旋转90°后得到△ACD,则点D的坐标是(7,3).查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 7.6×108 | B. | 0.76×10-9 | C. | 7.6×10-8 | D. | 0.76×109 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com