
【题目】如图①,点P是正方形ABCD的BC边上的一点,以DP为边长的正方形DEFP与正方形ABCD在BC的同侧,连接AC、FB.
(1)请你判断FB与AC又怎样的位置关系?并证明你的结论;
(2)若点P在射线CB上运动时,如图②,判断(1)中的结论FB与AC的位置关系是否仍然成立?并说明理由;
(3)当点P在直线CB上运动时,请你指出点E的运动路线,不必说明理由.
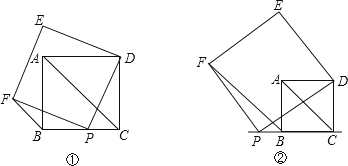
【答案】(1)FB∥AC,证明见解析;
(2)结论仍成立,理由见解析;
(3)当点P在直线BC上移动时,E的轨迹是图中的线段GA.
【解析】分析:(1)过F作FM⊥BC于M,证△PFM≌△DPC(AAS),推出DC=PM,FM=PC,求出∠FBM=45°即可.(2)中结论是还正确,过F作FM⊥BC于M,证△PFM≌△DPC(AAS),推出DC=PM,FM=PC,求出∠FBM=45°即可.(3)当点P在直线BC上移动时,E的轨迹是图中的线段GA,理由是△DCP绕D顺时针旋转90°,到达△DAE 即可以确定E的轨迹.
本题解析:(1)FB∥AC,
证明:过F作FM⊥BC于M,∵四边形ABCD、DEFP是正方形,∴∠ACB=45°,DC=BC,PF=DP,∠DCP=∠M=∠FPD=90°,
∴∠MFP+∠FPM=∠FPM+∠DPC=90°,∴∠MFP=∠CPD,
在△PFM和△DPC中:∠MFP=∠DPC,∠M=∠DCP, PF=DP
∴△PFM≌△DPC(AAS),∵DC=PM,FM=PC,∵DC=BC,
∴BC=DC=PM,∴PM-BP=BC-BP,∴BM=CP,∵FM=CP,∴FM=BM,∵∠M=90°,
∴∠FBM=∠MFB=0.5(180°-90°)=45°,∵∠ACB=45°,∴∠ACB=∠FBM,
∴FB∥AC;
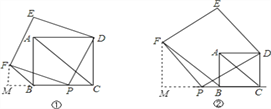
(2)结论仍成立,
理由是:过F作FM⊥BC于M,
∵四边形ABCD、DEFP是正方形,∴∠ACB=45°,DC=BC,PF=DP,∠DCP=∠M=∠FPD=90°,
∴∠MFP+∠FPM=∠FPM+∠DPC=90°,∴∠MFP=∠CPD,
在△PFM和△DPC中,
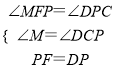 ,∴△PFM≌△DPC(AAS),
,∴△PFM≌△DPC(AAS),
∵DC=PM,FM=PC,∵DC=BC,∴BC=DC=PM,∴PM+BP=BC+BP,
∴BM=CP,∵FM=CP,∴FM=BM,∵∠M=90°,
∴∠FBM=∠MFB=0.5(180°-90°)=45°,∵∠ACB=45°,∴∠ACB=∠FBM,
∴FB∥AC;
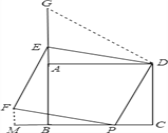
(3)当点P在直线BC上移动时,E的轨迹是图中的线段GA.


 高效智能课时作业系列答案
高效智能课时作业系列答案 捷径训练检测卷系列答案
捷径训练检测卷系列答案 小夫子全能检测系列答案
小夫子全能检测系列答案科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,点D为BC上一点,过A,B,D三点作⊙O,AE是⊙O的直径,AC是⊙O的切线,AD=DC,连结DE.
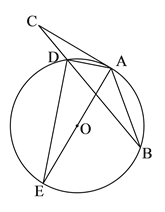
(1)求证:AB=AC;
(2)若![]() ,AC=
,AC=![]() ,求△ADE的周长.
,求△ADE的周长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一次测验中,初三(1)班的英语考试的平均分记为a分,所有高于平均分的学生的成绩减去平均分的分数之和记为m,所有低于平均分的学生的成绩与平均分相差的分数的绝对值的和记为n,则m与n的大小关系是______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一艘轮船以18海里/时的速度由西向东航行,在A处测得小岛C在北偏东75°方向上,两小时后,轮船在B处测得小岛C在北偏东60°方向上,在小岛周围15海里处有暗礁,若轮船仍然按18海里/时的速度向东航行,请问是否有触礁危险?并说明理由. 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在等边△ABC中,点F是AC边上一点,延长BC到点D,使BF=DF,若CD=CF,求证: 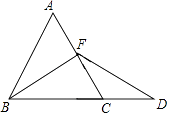
(1)点F为AC的中点;
(2)过点F作FE⊥BD,垂足为点E,请画出图形并证明BD=6CE.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】化简并求值:
(1)5(3a2b﹣ab2)﹣(ab2+3a2b),其中a=﹣![]() ,b=
,b=![]() .
.
(2)已知|x+1|+(y﹣2)2=0,求(2x2y﹣2xy2)﹣[(3x2y2+3x2y)+(3x2y2﹣3xy2)]的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2016年5月下旬,中国大数据博览会在贵阳举行,参加此次大会的人数约有89000人,将89000用科学记数法表示为( )
A.89×103
B.8.9×103
C.8.9×104
D.0.89×105
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com