
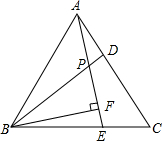
 如图,已知△ABC是等边三角形,D、E分别是AC、BC上的两点,AD=CE,且AE与BD交于点P,BF⊥AE于点F.
如图,已知△ABC是等边三角形,D、E分别是AC、BC上的两点,AD=CE,且AE与BD交于点P,BF⊥AE于点F.分析 (1)由等边三角形的性质得出AB=CA,∠BAD=∠ACE=60°,由SAS即可证明△ABD≌△CAE;
(2)由△ABD≌△CAE得出对应角相等∠ABD=∠CAE,根据三角形的外角性质得出∠BPF=60°,由含30°角的直角三角形的性质即可得出PF的长.
解答 (1)证明:∵△ABC是等边三角形,
∴AB=CA,∠BAD=∠ACE=60°,
在△ABD和△CAE中,
$\left\{\begin{array}{l}{AB=CA}&{\;}\\{∠BAD=∠ACE}&{\;}\\{AD=CE}&{\;}\end{array}\right.$,
∴△ABD≌△CAE(SAS);
(2)解:∵△ABD≌△CAE,
∴∠ABD=∠CAE,
∵∠BPF=∠BAP+∠ABD,
∴∠BPF=∠BAP+∠CAE=∠BAD=60°,
∵BF⊥AE,
∴∠PFB=90°,
∴∠PBF=30°,
∴PF=$\frac{1}{2}$BP=3.
点评 本题考查了等边三角形的性质、全等三角形的判定与性质、含30°角的直角三角形的性质;熟练掌握等边三角形的性质,证明三角形全等是解决问题的关键.


 智能训练练测考系列答案
智能训练练测考系列答案科目:初中数学 来源: 题型:解答题
 一天早上,马虎同学上学,到校后发现文具盒落在家里,此时离上课开始还有25分钟,于是立即步行回家取文具盒,同时,他爸爸从家里出发骑自行车以他3倍的速度给他送文具盒,两人在途中相遇,相遇后马虎立即坐父亲的自行车赶回学校.如图中线段AB、OB分别表示父子俩在送文具盒过程中,离学校的路程S(米)与所用时间t(分钟)之间的函数关系,结合图象解答下列问题(假设骑自行车和步行的速度始终保持不变);
一天早上,马虎同学上学,到校后发现文具盒落在家里,此时离上课开始还有25分钟,于是立即步行回家取文具盒,同时,他爸爸从家里出发骑自行车以他3倍的速度给他送文具盒,两人在途中相遇,相遇后马虎立即坐父亲的自行车赶回学校.如图中线段AB、OB分别表示父子俩在送文具盒过程中,离学校的路程S(米)与所用时间t(分钟)之间的函数关系,结合图象解答下列问题(假设骑自行车和步行的速度始终保持不变);查看答案和解析>>
科目:初中数学 来源: 题型:选择题
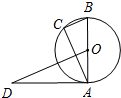 如图,AB是⊙O的直径,AD是⊙O的切线,BC∥OD交⊙O于点C,若AB=2,OD=3,则BC的长为( )
如图,AB是⊙O的直径,AD是⊙O的切线,BC∥OD交⊙O于点C,若AB=2,OD=3,则BC的长为( )| A. | $\frac{3}{2}$ | B. | $\frac{2}{3}$ | C. | $\frac{{\sqrt{3}}}{2}$ | D. | $\frac{{\sqrt{2}}}{2}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
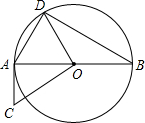 如图,AB是⊙O的直径,CA与⊙O相切于点A,点D在⊙O上,且OD⊥OC,
如图,AB是⊙O的直径,CA与⊙O相切于点A,点D在⊙O上,且OD⊥OC,查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
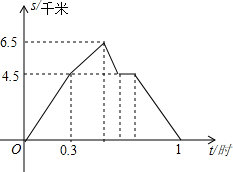 从A到B地的一条公路,先是一段平路,然后是一段上坡路,小明骑自行车从A地出发,到达B地后立即按原路返回A地,返回途中休息了一段时间,假设小明骑车在平路、上坡路、下坡路时分别保持匀速前进.已知小明骑自行车在上坡路的速度比平路上的速度每小时少5千米.下坡路的速度比在平路上的速度每小时多5千米,小明在去B地和返回A地两次经过C地的时间间隔为0.15小时,小明离A地的路程S(单位:千米)和出发的时间t(单位:小时)之间的函数关系式如图所示.下列说法中正确的个数为( )
从A到B地的一条公路,先是一段平路,然后是一段上坡路,小明骑自行车从A地出发,到达B地后立即按原路返回A地,返回途中休息了一段时间,假设小明骑车在平路、上坡路、下坡路时分别保持匀速前进.已知小明骑自行车在上坡路的速度比平路上的速度每小时少5千米.下坡路的速度比在平路上的速度每小时多5千米,小明在去B地和返回A地两次经过C地的时间间隔为0.15小时,小明离A地的路程S(单位:千米)和出发的时间t(单位:小时)之间的函数关系式如图所示.下列说法中正确的个数为( )| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com