
 一天早上,马虎同学上学,到校后发现文具盒落在家里,此时离上课开始还有25分钟,于是立即步行回家取文具盒,同时,他爸爸从家里出发骑自行车以他3倍的速度给他送文具盒,两人在途中相遇,相遇后马虎立即坐父亲的自行车赶回学校.如图中线段AB、OB分别表示父子俩在送文具盒过程中,离学校的路程S(米)与所用时间t(分钟)之间的函数关系,结合图象解答下列问题(假设骑自行车和步行的速度始终保持不变);
一天早上,马虎同学上学,到校后发现文具盒落在家里,此时离上课开始还有25分钟,于是立即步行回家取文具盒,同时,他爸爸从家里出发骑自行车以他3倍的速度给他送文具盒,两人在途中相遇,相遇后马虎立即坐父亲的自行车赶回学校.如图中线段AB、OB分别表示父子俩在送文具盒过程中,离学校的路程S(米)与所用时间t(分钟)之间的函数关系,结合图象解答下列问题(假设骑自行车和步行的速度始终保持不变);分析 (1)从图象可以看出,父子俩从出发到相遇花费了15分钟,路程是3600米,可以求出父子俩的速度,B点的纵坐标便可以求出,利用待定系数法便可以求出AB的解析式;
(2)从第一问中已经知道路程和速度求出父子俩赶回体育馆的时间就知道能否在比赛开始前到达体育馆了.
解答 解:(1)从图象可以看出:父子俩从出发到相遇时花费了15分钟,
设小明步行的速度为x米/分,则小明父亲骑车的速度为3x米/分,
依题意得:15x+45x=3600,
解得:x=60,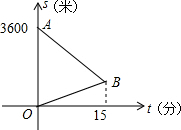
所以两人相遇处离体育馆的距离为60×15=900米,
所以点B的坐标为(15,900),
设直线AB的函数关系式为s=kt+b(k≠0)
由题意,直线AB经过点A(0,3600)、B(15,900)得:
$\left\{\begin{array}{l}{b=3600}\\{15k+b=900}\end{array}\right.$,
解得$\left\{\begin{array}{l}{k=-180}\\{b=3600}\end{array}\right.$,
∴直线AB的函数关系式为:S=-180t+3600;
(2)解法一:小明取票后,赶往体育馆的时间为:$\frac{900}{60×3}$,
小明取票花费的时间为:15+5=20分钟
∵20<25
∴小明能在比赛开始前到达体育馆.
点评 结合图象信息,读懂题目意思,从复杂的信息中分离出数学问题即相遇问题是解决本题的关键.另外本题也包含了生活实际与一次函数的联系问题.


 黄冈小状元解决问题天天练系列答案
黄冈小状元解决问题天天练系列答案 三点一测快乐周计划系列答案
三点一测快乐周计划系列答案科目:初中数学 来源: 题型:选择题
| A. | 从1,2,3,4,5这五个数中,任选两个数,所得两数的平方和是一个整数 | |
| B. | 从1,2,3,4,5这五个数中,任选两个数,所得两数的平方和是一个正整数的平方 | |
| C. | 从1,2,3,4,5这五个数中,任选两个数,所得两数的平方和是一个正整数的立方 | |
| D. | 从1,2,3,4,5这五个数中,任选两个数,所得两数的平方和是一个正整数的四次方 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 0.375 | B. | 0.6 | C. | 15 | D. | 25 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
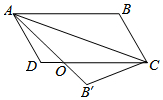 在平行四边形ABCD中,将△ABC沿AC对折,使点B落在B′处,AB′和CD相交
在平行四边形ABCD中,将△ABC沿AC对折,使点B落在B′处,AB′和CD相交查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
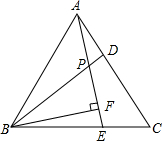 如图,已知△ABC是等边三角形,D、E分别是AC、BC上的两点,AD=CE,且AE与BD交于点P,BF⊥AE于点F.
如图,已知△ABC是等边三角形,D、E分别是AC、BC上的两点,AD=CE,且AE与BD交于点P,BF⊥AE于点F.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com