
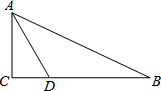
 在Rt△ABC中,∠C=90°,D为BC上一点,∠DAC=30°,BD=2,AB=2$\sqrt{3}$,则BC的长是3.
在Rt△ABC中,∠C=90°,D为BC上一点,∠DAC=30°,BD=2,AB=2$\sqrt{3}$,则BC的长是3. 科目:初中数学 来源: 题型:选择题
| A. | 甲 | B. | 乙 | C. | 丙 | D. | 丁 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 一天早上,马虎同学上学,到校后发现文具盒落在家里,此时离上课开始还有25分钟,于是立即步行回家取文具盒,同时,他爸爸从家里出发骑自行车以他3倍的速度给他送文具盒,两人在途中相遇,相遇后马虎立即坐父亲的自行车赶回学校.如图中线段AB、OB分别表示父子俩在送文具盒过程中,离学校的路程S(米)与所用时间t(分钟)之间的函数关系,结合图象解答下列问题(假设骑自行车和步行的速度始终保持不变);
一天早上,马虎同学上学,到校后发现文具盒落在家里,此时离上课开始还有25分钟,于是立即步行回家取文具盒,同时,他爸爸从家里出发骑自行车以他3倍的速度给他送文具盒,两人在途中相遇,相遇后马虎立即坐父亲的自行车赶回学校.如图中线段AB、OB分别表示父子俩在送文具盒过程中,离学校的路程S(米)与所用时间t(分钟)之间的函数关系,结合图象解答下列问题(假设骑自行车和步行的速度始终保持不变);查看答案和解析>>
科目:初中数学 来源: 题型:解答题
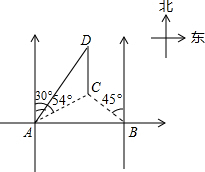 如图,在海岸边相距12km的两个观测站A、B,同时观测到一货船C的方向角分别为北偏东54°和北偏西45°,该货船向正北航行,与此同时A观测站处派出一快艇以70km/h的速度沿北偏东30°方向追赶货船送上一批货物,正好在D处追上货船,求快艇追赶的时间.(参考数据:sin54°≈0.8,cos54°≈0.6,tan54°≈1.4)
如图,在海岸边相距12km的两个观测站A、B,同时观测到一货船C的方向角分别为北偏东54°和北偏西45°,该货船向正北航行,与此同时A观测站处派出一快艇以70km/h的速度沿北偏东30°方向追赶货船送上一批货物,正好在D处追上货船,求快艇追赶的时间.(参考数据:sin54°≈0.8,cos54°≈0.6,tan54°≈1.4)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
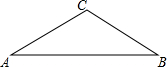 如图,已知在等腰△ABC中,∠C=120°
如图,已知在等腰△ABC中,∠C=120°查看答案和解析>>
科目:初中数学 来源: 题型:选择题
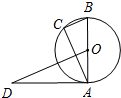 如图,AB是⊙O的直径,AD是⊙O的切线,BC∥OD交⊙O于点C,若AB=2,OD=3,则BC的长为( )
如图,AB是⊙O的直径,AD是⊙O的切线,BC∥OD交⊙O于点C,若AB=2,OD=3,则BC的长为( )| A. | $\frac{3}{2}$ | B. | $\frac{2}{3}$ | C. | $\frac{{\sqrt{3}}}{2}$ | D. | $\frac{{\sqrt{2}}}{2}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
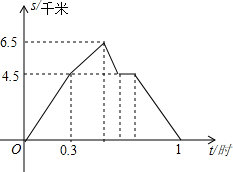 从A到B地的一条公路,先是一段平路,然后是一段上坡路,小明骑自行车从A地出发,到达B地后立即按原路返回A地,返回途中休息了一段时间,假设小明骑车在平路、上坡路、下坡路时分别保持匀速前进.已知小明骑自行车在上坡路的速度比平路上的速度每小时少5千米.下坡路的速度比在平路上的速度每小时多5千米,小明在去B地和返回A地两次经过C地的时间间隔为0.15小时,小明离A地的路程S(单位:千米)和出发的时间t(单位:小时)之间的函数关系式如图所示.下列说法中正确的个数为( )
从A到B地的一条公路,先是一段平路,然后是一段上坡路,小明骑自行车从A地出发,到达B地后立即按原路返回A地,返回途中休息了一段时间,假设小明骑车在平路、上坡路、下坡路时分别保持匀速前进.已知小明骑自行车在上坡路的速度比平路上的速度每小时少5千米.下坡路的速度比在平路上的速度每小时多5千米,小明在去B地和返回A地两次经过C地的时间间隔为0.15小时,小明离A地的路程S(单位:千米)和出发的时间t(单位:小时)之间的函数关系式如图所示.下列说法中正确的个数为( )| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com