
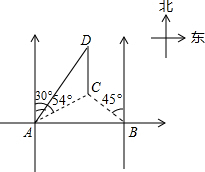
 如图,在海岸边相距12km的两个观测站A、B,同时观测到一货船C的方向角分别为北偏东54°和北偏西45°,该货船向正北航行,与此同时A观测站处派出一快艇以70km/h的速度沿北偏东30°方向追赶货船送上一批货物,正好在D处追上货船,求快艇追赶的时间.(参考数据:sin54°≈0.8,cos54°≈0.6,tan54°≈1.4)
如图,在海岸边相距12km的两个观测站A、B,同时观测到一货船C的方向角分别为北偏东54°和北偏西45°,该货船向正北航行,与此同时A观测站处派出一快艇以70km/h的速度沿北偏东30°方向追赶货船送上一批货物,正好在D处追上货船,求快艇追赶的时间.(参考数据:sin54°≈0.8,cos54°≈0.6,tan54°≈1.4) 分析 延长DC交AB于E,那么DE⊥AB,CE为直角△ACE和△CEB的公共直角边,可用CE表示出AE和EB,然后根据AB的长来求出CE的长,进而求得AE的长,那么就能在直角△ADE中,根据三角函数求出AD的长,即可求出时间.
解答 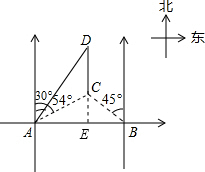 解:延长DC交AB于E,那么DE⊥AB.
解:延长DC交AB于E,那么DE⊥AB.
∵直角三角形ACE中,∠AEC=90°,∠ACE=54°,
∴AE=CE•tan54°≈1.4CE.
∵在直角三角形CEB中,∠BEC=90°,∠CBE=45°,
∴BE=CE.
∴AB=AE+BE=1.4CE+CE=12,
∴CE=5,
∴AE=1.4×5=7.
∵直角三角形ADE中,∠AED=90°,∠ADE=30°,
∴AD=AE÷sin30°=2AE=14.
因此快艇追赶的时间应该是14÷70=0.2小时.
点评 本题考查了解直角三角形的应用-方向角问题,锐角三角函数的定义,准确作出辅助线构造直角三角形是解题的关键.


 挑战100单元检测试卷系列答案
挑战100单元检测试卷系列答案科目:初中数学 来源: 题型:选择题
| A. | 0.375 | B. | 0.6 | C. | 15 | D. | 25 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
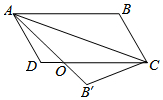 在平行四边形ABCD中,将△ABC沿AC对折,使点B落在B′处,AB′和CD相交
在平行四边形ABCD中,将△ABC沿AC对折,使点B落在B′处,AB′和CD相交查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 3.6 | B. | 4.3 | C. | 3.3 | D. | 4.4 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | k>0,b>0 | B. | k>0,b<0 | C. | k<0,b<0 | D. | k<0,b>0 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com