
【题目】如图,⊙C经过原点且与两坐标轴分别交于点A和点B,点A的坐标为(0,3),D为⊙C在第一象限内的一点且∠ODB=60°.
求:(1)求线段AB的长及⊙C的半径;
(2)求B点坐标及圆心C的坐标.

【答案】(1)6,3;(2)(3![]() ,0),(
,0),(![]() ,
,![]() )
)
【解析】
(1)在Rt△OAB中,只要证明∠OAB=∠ODB=60°,利用直角三角形30度角性质即可解决问题.
(2)过C点作CE⊥OB于E,利用直角三角形30度角性质求出OB的长,再利用垂径定理以及三角形中位线定理求出CE即可解决问题.
(1)∵点A的坐标为(0,3),∴OA=3.
∵∠ODB=∠OAB,∠ODB=60°,∴∠OAB=60°.
∵∠AOB是直角,∴AB是⊙C的直径,∴∠OBA=30°,∴AB=2OA=6,∴⊙C的半径r=3;
(2)过C点作CE⊥OB于E.在Rt△OAB中,∠OBA=30°,∴OB=![]() AB=
AB=![]() ×6=3
×6=3![]() ,∴B的坐标为:(3
,∴B的坐标为:(3![]() ,0),由垂径定理得:OE=
,0),由垂径定理得:OE=![]() OB=
OB=![]() .
.
∵AC=BC,OE=BE,∴CE=![]() OA=
OA=![]() ×3=
×3=![]() ,∴C的坐标为(
,∴C的坐标为(![]() ).
).


科目:初中数学 来源: 题型:
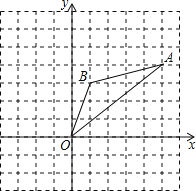
【题目】如图,在边长为1的正方形组成的网格中,△AOB的顶点均在格点上,其中点A(5,4),B(1,3),将△AOB绕点O逆时针旋转90°后得到△A1OB1.
(1)画出△A1OB1;
(2)在旋转过程中点B所经过的路径长为______;
(3)求在旋转过程中线段AB、BO扫过的图形的面积之和.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】太原是一座具有4700多年历史、2500年建城史的历史古都,系有“锦绣太原城”的美誉,在“我可爱的家乡”主题班会中,主持人准备了“晋祠园林”、“崇山大佛”、“龙山石窟”、“凌霄双塔”这四处景点的照片各一张,并将它们背面朝上放置(照片背面完全相同),甲同学从中随机抽取一张,不放回,乙再从剩下的照片中随机抽取一张,若要根据抽取的照片作相关景点介绍,求甲、乙两人中恰好有一人介绍“晋祠园林”的概率.(提示:可用照片序号列表或画树状图)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,![]() 为等腰直角三角形,
为等腰直角三角形,![]() ,
,![]() .
.

(1)如图1,直接写出![]() 点的坐标;
点的坐标;
(2)如图2,若![]() 为
为![]() 边上一动点,连接
边上一动点,连接![]() ,过
,过![]() 作
作![]() ,交
,交![]() 于点
于点![]() ,交
,交![]() 于点
于点![]() ,点
,点![]() 是
是![]() 的中点,连接
的中点,连接![]() 、
、![]() ,猜想
,猜想![]() 的度数,并说明理由.
的度数,并说明理由.
(3)如图3,在(2)的条件下,过点![]() 作
作![]() ,交
,交![]() 轴于点
轴于点![]() ,连接
,连接![]() ,当点
,当点![]() 在边
在边![]() 上(不含端点)运动过程中,等式
上(不含端点)运动过程中,等式![]() 是否成立?若成立,请证明:若不成立,说明理由.
是否成立?若成立,请证明:若不成立,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
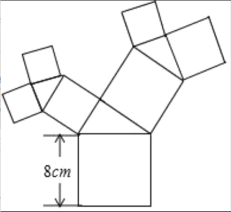
【题目】如图所示的图形中,所有的四边形都是正方形,所有的三角形都是直角三角形,其中最大的正方形的边长为![]() ,则图中所有正方形的面积的和是___________
,则图中所有正方形的面积的和是___________![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
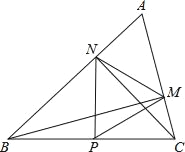
【题目】如图,在△ABC中∠A=60°,BM⊥AC于点M,CN⊥AB于点N,P为BC边的中点,连接PM,PN,则下列结论:①PM=PN;②![]() ;③△PMN为等边三角形;④当∠ABC=45°时,BN=
;③△PMN为等边三角形;④当∠ABC=45°时,BN=![]() PC.其中正确的个数是( )
PC.其中正确的个数是( )
A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
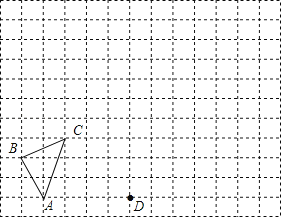
【题目】如图,在由边长为1的单位正方形组成的网格中,按要求画出坐标系及△A1B1C1及△A2B2C2;
(1)若点A、C的坐标分别为(﹣3,0)、(﹣2,3),请画出平面直角坐标系并指出点B的坐标;
(2)画出△ABC关于y轴对称再向上平移1个单位后的图形△A1B1C1;
(3)以图中的点D为位似中心,将△A1B1C1作位似变换且把边长放大到原来的两倍,得到△A2B2C2.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】创新需要每个人的参与,就拿小华来说,为了解决晒衣服的,聪明的他想到了一个好办法,在家宽敞的院内地面![]() 上立两根等长的立柱
上立两根等长的立柱![]() 、
、![]() (均与地面垂直),并在立柱之间悬挂一根绳子.由于挂的衣服比较多,绳子的形状近似成了抛物线
(均与地面垂直),并在立柱之间悬挂一根绳子.由于挂的衣服比较多,绳子的形状近似成了抛物线![]() ,如图
,如图![]() ,已知立柱
,已知立柱![]() 米,
米, ![]() 米.
米.
(1)求绳子最低点离地面的距离;
(2)为了防止衣服碰到地面,小华在离![]() 为
为![]() 米的位置处用一根垂直于地面的立柱
米的位置处用一根垂直于地面的立柱![]() 撑起绳子 (如图2),使左边抛物线
撑起绳子 (如图2),使左边抛物线![]() 的最低点距
的最低点距![]() 为
为![]() 米,离地面
米,离地面![]() 米,求
米,求![]() 的长.
的长.
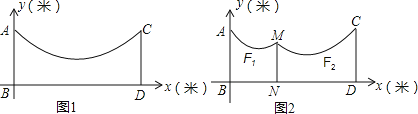
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,折叠矩形ABCD,使点B落在对角线AC上的点F处,若BC=8,AB=6,则线段CE的长度是( )

A. 3 B. 4 C. 5 D. 6
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com