Question

13．探究与发现：如图1所示的图形，像我们常见的学习用品--圆规．我们不妨把这样图形叫做“规形图”，
（1）观察“规形图”，试探究∠BDC与∠A、∠B、∠C之间的关系，并说明理由；
（2）请你直接利用以上结论，解决以下三个问题：
①如图2，把一块三角尺XYZ放置在△ABC上，使三角尺的两条直角边XY、XZ恰好经过点B、C，∠A=40°，则∠ABX+∠ACX=50°；
②如图3，DC平分∠ADB，EC平分∠AEB，若∠DAE=40°，∠DBE=130°，求∠DCE的度数；
③如图4，∠ABD，∠ACD的10等分线相交于点G₁、G₂…、G₉，若∠BDC=133°，∠BG₁C=70°，求∠A的度数．

Answer 1

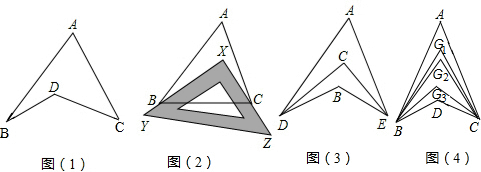
分析 （1）首先连接AD并延长至点F，然后根据外角的性质，即可判断出∠BDC=∠A+∠B+∠C．
（2）①由（1）可得∠ABX+∠ACX+∠A=∠BXC，然后根据∠A=40°，∠BXC=90°，求出∠ABX+∠ACX的值是多少即可．
②由（1）可得∠DBE=∠DAE+∠ADB+∠AEB，再根据∠DAE=40°，∠DBE=130°，求出∠ADB+∠AEB的值是多少；然后根据∠DCE=$\frac{1}{2}$（∠ADB+∠AEB）+∠DAE，求出∠DCE的度数是多少即可．
③根据∠BG₁C=$\frac{1}{10}$（∠ABD+∠ACD）+∠A，∠BG₁C=70°，设∠A为x°，可得∠ABD+∠ACD=133°-x°，解方程，求出x的值，即可判断出∠A的度数是多少．

解答 解：（1）如图（1），连接AD并延长至点F，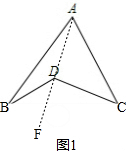
，
根据外角的性质，可得
∠BDF=∠BAD+∠B，∠CDF=∠C+∠CAD，
又∵∠BDC=∠BDF+∠CDF，∠BAC=∠BAD+∠CAD，
∴∠BDC=∠A+∠B+∠C；

（2）①由（1），可得
∠ABX+∠ACX+∠A=∠BXC，
∵∠A=40°，∠BXC=90°，
∴∠ABX+∠ACX=90°-40°=50°，
故答案为：50．

②由（1），可得
∠DBE=∠DAE+∠ADB+∠AEB，
∴∠ADB+∠AEB=∠DBE-∠DAE=130°-40°=90°，
∴$\frac{1}{2}$（∠ADB+∠AEB）=90°÷2=45°，
∴∠DCE=$\frac{1}{2}$（∠ADB+∠AEB）+∠DAE
=45°+40°
=85°；

③∠BG₁C=$\frac{1}{10}$（∠ABD+∠ACD）+∠A，
∵∠BG₁C=70°，
∴设∠A为x°，
∵∠ABD+∠ACD=133°-x°
∴$\frac{1}{10}$（133-x）+x=70，
∴13.3-$\frac{1}{10}$x+x=70，
解得x=63，
即∠A的度数为63°．

点评 此题主要考查了三角形的内角和定理，利用三角形的内角和定理和外角的性质是解答此题的关键．