
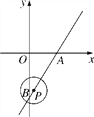
【题目】如图,在平面直角坐标系xOy中,直线y=![]() x-2
x-2![]() 与x轴、y轴分别交于A,B两点,P是直线AB上一动点,⊙P的半径为1.
与x轴、y轴分别交于A,B两点,P是直线AB上一动点,⊙P的半径为1.
(1)判断原点O与⊙P的位置关系,并说明理由;
(2)当⊙P过点B时,求⊙P被y轴所截得的劣弧的长;
(3)当⊙P与x轴相切时,求出切点的坐标.
【答案】(1)原点O在⊙P外 (2)![]() (3)
(3)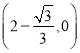 或
或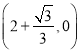
解:(1)原点O在⊙P外.理由如下:∵直线y=![]() x-2
x-2![]() 与x轴、y轴分别交于A,B两点,∴点A的坐标为(2,0),点B的坐标为(0,-2
与x轴、y轴分别交于A,B两点,∴点A的坐标为(2,0),点B的坐标为(0,-2![]() ).在Rt△OAB中,tan∠OBA=
).在Rt△OAB中,tan∠OBA=![]() =
=![]() =
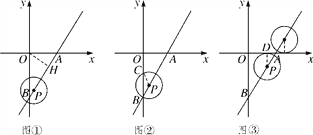
=![]() ,∴∠OBA=30°.如图①,过点O作OH⊥AB于点H,在Rt△OBH中,OH=OB·sin∠OBA=
,∴∠OBA=30°.如图①,过点O作OH⊥AB于点H,在Rt△OBH中,OH=OB·sin∠OBA=![]() .∵
.∵![]() >1,∴原点O在⊙P外;
>1,∴原点O在⊙P外;
(2)如图②,当⊙P过点B时,点P在y轴右侧时,∵PB=PC,∴∠PCB=∠OBA=30°,∴⊙P被y轴所截的劣弧所对的圆心角的度数为180°-30°-30°=120°,∴弧长为![]() =
=![]() ;同理:当⊙P过点B时,点P在y轴左侧时,弧长同样为
;同理:当⊙P过点B时,点P在y轴左侧时,弧长同样为![]() .∴当⊙P过点B时,⊙P被y轴所截得的劣弧的长为
.∴当⊙P过点B时,⊙P被y轴所截得的劣弧的长为![]() ;
;
(3)如图③,当⊙P与x轴相切时,且位于x轴下方时,设切点为D,作PD⊥x轴,∴PD∥y轴,∴∠APD=∠ABO=30°.在Rt△DAP中,AD=DP·tan∠DPA=1×tan30°=![]() ,∴OD=OA-AD=2-
,∴OD=OA-AD=2-![]() ,∴此时点D的坐标为
,∴此时点D的坐标为![]() ;当⊙P与x轴相切时,且位于x轴上方时,根据对称性可以求得此时切点的坐标为
;当⊙P与x轴相切时,且位于x轴上方时,根据对称性可以求得此时切点的坐标为![]() .综上所述,当⊙P与x轴相切时,切点的坐标为
.综上所述,当⊙P与x轴相切时,切点的坐标为![]() 或
或![]() .
.

【解析】试题分析: ![]() 由直线
由直线![]() 与
与![]() 轴、
轴、![]() 轴分别交于
轴分别交于![]() 两点,可求得点
两点,可求得点![]() 与点
与点![]() 的坐标,继而求得∠OBA=30°.然后过点O作OH⊥AB于点H,利用三角函数可求得
的坐标,继而求得∠OBA=30°.然后过点O作OH⊥AB于点H,利用三角函数可求得![]() 的长,继而求得答案;
的长,继而求得答案;
![]() 当⊙P过点B时,点P在y轴右侧时,⊙P被y轴所截的劣弧所对的圆心角的度数为180°-30°-30°=120°,则可求得弧长;同理可求得⊙P过点B时,点P在y轴左侧时, ⊙P被y轴所截的劣弧的长;
当⊙P过点B时,点P在y轴右侧时,⊙P被y轴所截的劣弧所对的圆心角的度数为180°-30°-30°=120°,则可求得弧长;同理可求得⊙P过点B时,点P在y轴左侧时, ⊙P被y轴所截的劣弧的长;
![]() 首先求得⊙P与x轴相切时,且位于x轴下方时,设切点为D,求出点D的坐标,然后利用对称性可以求得当⊙P与x轴相切时,且位于x轴上方时,点D的坐标.
首先求得⊙P与x轴相切时,且位于x轴下方时,设切点为D,求出点D的坐标,然后利用对称性可以求得当⊙P与x轴相切时,且位于x轴上方时,点D的坐标.
试题解析:(1)原点O在⊙P外.
理由如下:∵直线![]() 与x轴、y轴分别交于A,B两点,
与x轴、y轴分别交于A,B两点,
∴点A的坐标为(2,0),点B的坐标为![]()
在Rt△OAB中, ![]()
∴∠OBA=30°.
如图①,过点O作OH⊥AB于点H,
在Rt△OBH中, ![]()
![]() ∴原点O在⊙P外;
∴原点O在⊙P外;
(2)如图②,当⊙P过点B时,点P在y轴右侧时,
∵PB=PC,∴∠PCB=∠OBA=30°,
∴⊙P被y轴所截的劣弧所对的圆心角的度数为180°-30°-30°=120°,
∴弧长为: ![]()
同理:当⊙P过点B时,点P在y轴左侧时,弧长同样为![]()
∴当⊙P过点B时,⊙P被y轴所截得的劣弧的长为![]()
(3)如图③,当⊙P与x轴相切时,且位于x轴下方时,设切点为D,作PD⊥x轴,∴PD∥y轴,∴∠APD=∠ABO=30°.
在Rt△DAP中, ![]()
![]()
∴此时点D的坐标为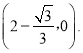
当⊙P与x轴相切时,且位于x轴上方时,根据对称性可以求得此时切点的坐标为
综上所述,当⊙P与x轴相切时,切点的坐标为 或
或 .
.


科目:初中数学 来源: 题型:
【题目】某人购进一批苹果,到市场零售,已知卖出苹果数量x与售价y的关系如下表,写出用x表示y的关系式______.
数量x(千克) | 2 | 3 | 4 | 5 |
售价y(元) | 16.2 | 24.3 | 32.4 | 40.5 |
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,某人为了测量小山顶上的塔ED的高,他在山下的点A处测得塔尖点D的仰角为45°,再沿AC方向前进60m到达山脚点B,测得塔尖点D的仰角为60°,塔底点E的仰角为30°,求塔ED的高度.(结果保留根号)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】生物学家发现了一种病毒,其长度约为0.00000032mm,数据0.00000032用科学记数法表示正确的是( )
A.3.2×107
B.3.2×108
C.3.2×10﹣7
D.3.2×10﹣8
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】工人师傅用一块长为10dm,宽为6dm的矩形铁皮制作一个无盖的长方体容器,需要将四角各裁掉一个正方形.(厚度不计)

(1)在图中画出裁剪示意图,用实线表示裁剪线,虚线表示折痕;并求长方体底面面积为12dm2时,裁掉的正方形边长多大?
(2)若要求制作的长方体的底面长不大于底面宽的五倍,并将容器进行防锈处理,侧面每平方分米的费用为0.5元,底面每平方分米的费用为2元,裁掉的正方形边长多大时,总费用最低,最低为多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某报纸上刊登了一则新闻,“某种品牌的节能灯的合格率为95%”,请据此回答下列问题:
(1)这则新闻是否说明市面上所有这种品牌的节能灯恰有5%为不合格?
(2)你认为这则消息来源于普查,还是抽样调查?为什么?
(3)如果已知在这次检查中合格产品有76个,则共有多少个节能灯接受检查?
(4)如果此次检查了两种产品,数据如下表所示,有人由此认为“A品牌的不合格率比B品牌低,更让人放心”.你同意这种说法吗?为什么?
品牌 | A品牌 | B品牌 |
被检测数 | 70 | 10 |
不合格数 | 3 | 1 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com