
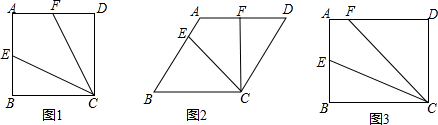
分析 (1)根据含30°的直角三角形的性质解答即可;
(2)过E作EG⊥BC,利用含30°的直角三角形的性质和等腰直角三角形的性质进行解答即可;
(3)延长FE交CB延长线于点M,再利用相似三角形的性质和勾股定理进行解答.
解答 解:(1)∵四边形ABCD是正方形,∠DFC=60°,
∴∠DCF=30°,
∵∠DFC=2∠FCE,
∴∠FCE=∠ECB=30°,
∴BC=4$\sqrt{3}$,
∴DF=4,
∴AF=$4\sqrt{3}-4$;
故答案为:$4\sqrt{3}-4$;
(2)过E作EG⊥BC,如图1: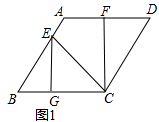
∵∠DFC=90°,∠DFC=2∠FCE,
∴∠FCE=∠BCE=45°,
∵∠A=120°,
∴∠B=60°,
∴BG=2,EG=$2\sqrt{3}$,
∴GC=EG=$2\sqrt{3}$,
∴BC=CD=AB=AD=$2+2\sqrt{3}$,
∴DF=$\frac{1}{2}AD$=1+$\sqrt{3}$,
∴AF=1+$\sqrt{3}$,
∴AE=AB-BE=2+2$\sqrt{3}$-4=2$\sqrt{3}$-2,
∴$\frac{AF}{AE}=\frac{1+\sqrt{3}}{2\sqrt{3}-2}=\frac{2+\sqrt{3}}{2}$;
(3)延长FE交CB延长线于点M,如图2:
在△AFE与△BME中,
$\left\{\begin{array}{l}{∠EBM=∠EAF=90°}\\{EB=AE}\\{∠BEM=∠AEF}\end{array}\right.$,
∴△AFE≌△BME(ASA),
∴BM=AF,ME=EF,
∵∠DFC=2∠FCE,
∴CE是∠FCB的角平分线,
∴CM=CF=13,
在Rt△MEC中,ME=$\sqrt{M{C}^{2}-C{E}^{2}}=\sqrt{1{3}^{2}-1{2}^{2}}=5$,
∵∠EMB=∠EMB,∠EBM=∠EBC=90°,
∴△EMB∽△EMC,
∴$\frac{AF}{AE}=\frac{BM}{BE}=\frac{ME}{CE}=\frac{5}{12}$.
点评 此题考查四边形综合题,关键是根据全等三角形和相似三角形的判定和性质进行分析.


科目:初中数学 来源: 题型:选择题
 如图,已知:∠MON=30°,点A1、A2、A3、…在射线ON上,点B1、B2、B3、…在射线OM上,△A1B1A2、△A2B2A3、△A3B3A4、…均为等边三角形,若OA1=1,则△A9B9A10的边长为( )
如图,已知:∠MON=30°,点A1、A2、A3、…在射线ON上,点B1、B2、B3、…在射线OM上,△A1B1A2、△A2B2A3、△A3B3A4、…均为等边三角形,若OA1=1,则△A9B9A10的边长为( )| A. | 32 | B. | 64 | C. | 128 | D. | 256 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
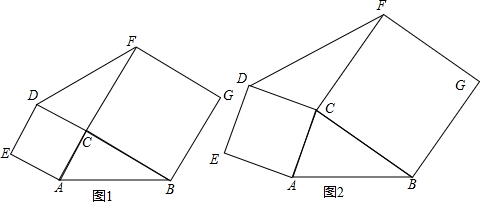
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | (x+2)2=x2+4 | B. | (x-1)(-1-x)=x2-1 | C. | (-2x+1)2=4x2+4x+1 | D. | (x-1)(x-2)=x2-3x+2 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
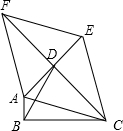 定义:只有一组对角是直角的四边形叫做损矩形,连接它的两个非直角顶点的线段叫做这个损矩形的直径,即损矩形外接圆的直径.如图,△ABC中,∠ABC=90°,以AC为一边向形外作菱形ACEF,点D是菱形ACEF对角线的交点,连接BD.若∠DBC=60°,∠ACB=15°,BD=2$\sqrt{3}$,则菱形ACEF的面积为12$\sqrt{3}$.
定义:只有一组对角是直角的四边形叫做损矩形,连接它的两个非直角顶点的线段叫做这个损矩形的直径,即损矩形外接圆的直径.如图,△ABC中,∠ABC=90°,以AC为一边向形外作菱形ACEF,点D是菱形ACEF对角线的交点,连接BD.若∠DBC=60°,∠ACB=15°,BD=2$\sqrt{3}$,则菱形ACEF的面积为12$\sqrt{3}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 小华从家里到学校的路是一段平路和一段下坡路,假设他始终保持平路每分钟走60m,下坡路每分钟走80m,上坡路每分钟走40m,则他从家里到学校需10min,从学校到家里需15min.问:从小华家到学校的平路和下坡路各有多远?
小华从家里到学校的路是一段平路和一段下坡路,假设他始终保持平路每分钟走60m,下坡路每分钟走80m,上坡路每分钟走40m,则他从家里到学校需10min,从学校到家里需15min.问:从小华家到学校的平路和下坡路各有多远?查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com