
分析 (1)根据题目中的式子的变化规律可以写出第四个等式;
(2)根据题目中的式子的变化规律可以猜想出第n个等式并加以证明.
解答 解:(1)由题目中式子的变化规律可得,
第四个等式是:$\frac{{5}^{2}-{4}^{2}-1}{2}=4$;
(2)第n个等式是:$\frac{(n+1)^{2}-{n}^{2}-1}{2}=n$,
证明:∵$\frac{(n+1)^{2}-{n}^{2}-1}{2}$
=$\frac{[(n+1)+n][(n+1)-n]-1}{2}$
=$\frac{2n+1-1}{2}$
=$\frac{2n}{2}$
=n,
∴第n个等式是:$\frac{(n+1)^{2}-{n}^{2}-1}{2}=n$.
点评 本题考查规律型:数字的变化类,解答本题的关键是明确题目中式子的变化规律,求出相应的式子.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
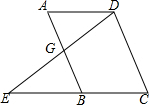 (1)已知:如图所示,AB∥CD,∠A=∠C,求证:BC∥AD
(1)已知:如图所示,AB∥CD,∠A=∠C,求证:BC∥AD查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | ab-b=b(a-1) | B. | (m+n)(m-n)=m2-n2 | C. | -10x-10=-10(x-1) | D. | x2-2x+1=x(x-2)+1 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | ①③④ | B. | ②③ | C. | ①②④ | D. | ①②③ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com