
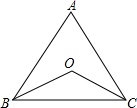
 如图所示,在△ABC中,AB=AC,∠ABC和∠ACB的平分线相交于点O.试判断△OBC的形状,并说明理由.
如图所示,在△ABC中,AB=AC,∠ABC和∠ACB的平分线相交于点O.试判断△OBC的形状,并说明理由.科目:初中数学 来源: 题型:
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 2 |
查看答案和解析>>
科目:初中数学 来源: 题型:
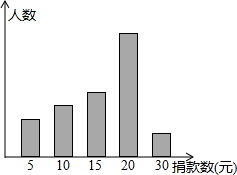 某中学对“助残”自愿捐款活动进行抽样调查,得到一组学生捐款情况的数据,如图是根据这组数据绘制的统计图,图中从左到右各长方形高度之比为3:4:5:8:2,又知此次调查中捐15元和20元得人数共39人.
某中学对“助残”自愿捐款活动进行抽样调查,得到一组学生捐款情况的数据,如图是根据这组数据绘制的统计图,图中从左到右各长方形高度之比为3:4:5:8:2,又知此次调查中捐15元和20元得人数共39人.查看答案和解析>>
科目:初中数学 来源: 题型:
| π |
| 3 |
| 22 |
| 3 |
| 7 |
| 3 | -27 |
| 3 | 9 |
| 0.4 |
| 16 |
| 2 |
| (-3)2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com