
【题目】如图,正方形ABCD中,对角线AC、BD交于点O,将BD绕点B逆时针旋转30°到BE所在的位置,BE与AD交于点F,分别连接DE、CE.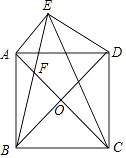
(1)求证:DE=DF;
(2)求证:AE∥BD;
(3)求tan∠ACE的值.
【答案】
(1)
证明:∵BD绕点B逆时针旋转30°到BE,
∴∠DBE=30°,BD=BE,
∴∠BDE=∠BED= ![]() =75°,
=75°,
在正方形ABCD中,BD是对角线,
∴∠ADB=45°,
∴∠EDF=75°﹣45°=30°,
在△DEF中,∠DFE=180°﹣∠EDF﹣∠FED=180°﹣30°﹣75°=75°,
∴∠DFE=∠DEF,
∴DE=DF
(2)
证明:过E作EG⊥BD于点G,

∵∠DBE=30°,
∴EG= ![]() BE=
BE= ![]() BD,
BD,
在正方形ABCD中,AC、BD是对角线,
∴AC=BD,OA= ![]() AC=
AC= ![]() BD,AC⊥BD,
BD,AC⊥BD,
∴EG=OA,且EG∥OA,
∴四边形AOGE是平行四边形,
∵∠AOD=90°,
∴四边形AOGE是矩形,
∴AE∥BD:
(3)
设EG=x,则BE=BD=AC=2EG=2x,
Rt△BEG中,BG= ![]() =
= ![]() x,
x,
∴OG=BG﹣BO=( ![]() ﹣1)x,
﹣1)x,
在矩形AOGE中,∠EAO=90°
∴AE=OG=( ![]() ﹣1)x,
﹣1)x,
∴tan∠ACE= ![]() =
= ![]() .
.
【解析】(1)先根据旋转的性质得∠DBE=30°,BD=BE,求∠BDE=∠BED=75°,则∠EDF=75°﹣45°=30°,根据三角形的内角和得:∠DFE=75°,所以∠DFE=∠DEF,由等角对等边得结论;(2)如图所示,作辅助线,构建直角三角形,根据直角三角形30°角的性质得:EG= ![]() BE=
BE= ![]() BD,由正方形的性质得:AC=BD,OA=
BD,由正方形的性质得:AC=BD,OA= ![]() AC=
AC= ![]() BD,根据一组对边平行且相等的四边形是平行四边形证明四边形AOGE是平行四边形,则AE∥BD;(3)证明四边形AOGE是矩形,设EG=x,由勾股定理得:BG=
BD,根据一组对边平行且相等的四边形是平行四边形证明四边形AOGE是平行四边形,则AE∥BD;(3)证明四边形AOGE是矩形,设EG=x,由勾股定理得:BG= ![]() =
= ![]() x,由矩形AOGE可知:∠EAO=90°,计算tan∠ACE的值即可.
x,由矩形AOGE可知:∠EAO=90°,计算tan∠ACE的值即可.
【考点精析】利用三角形三边关系和正方形的性质对题目进行判断即可得到答案,需要熟知三角形两边之和大于第三边;三角形两边之差小于第三边;不符合定理的三条线段,不能组成三角形的三边;正方形四个角都是直角,四条边都相等;正方形的两条对角线相等,并且互相垂直平分,每条对角线平分一组对角;正方形的一条对角线把正方形分成两个全等的等腰直角三角形;正方形的对角线与边的夹角是45o;正方形的两条对角线把这个正方形分成四个全等的等腰直角三角形.


科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠B=90°,∠A=30°,以点A为圆心,BC长为半径画弧交AB于点D,分别以点A、D为圆心,AB长为半径画弧,两弧交于点E,连接AE,DE,则∠EAD的余弦值是( ) 
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y= ![]() x2﹣
x2﹣ ![]() x+c与y轴交于点A(0,﹣
x+c与y轴交于点A(0,﹣ ![]() ),与x轴交于B、C两点,其对称轴与x轴交于点D,直线l∥AB且过点D.
),与x轴交于B、C两点,其对称轴与x轴交于点D,直线l∥AB且过点D.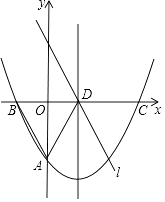
(1)求AB所在直线的函数表达式;
(2)请你判断△ABD的形状并证明你的结论;
(3)点E在线段AD上运动且与点A、D不重合,点F在直线l上运动,且∠BEF=60°,连接BF,求出△BEF面积的最小值.
解:
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】解方程:![]() -
-![]() =1-
=1-![]()
解:去分母,得_________________________________.
去括号,得___________________________.
移项,得___________________________.
合并同类项,得__________.
两边都除以______,得x=_______.
查看答案和解析>>
科目:初中数学 来源: 题型:
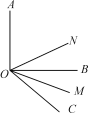
【题目】(1)如图,∠AOB=90°,∠BOC=40°,ON平分∠AOC,OM平分∠BOC,求∠MON的度数;
(2)如果(1)中∠BOC=α,且α<90°,其他条件不变,求∠MON的度数;
(3)如果(1)中∠AOB=β,且β<90°,其他条件不变,求∠MON的度数;
(4)从(1)(2)(3)的结果中能得到什么规律?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若 a、b、c 为△ABC 的三边,且满足 a2+b2+c2=ab+ac+bc.点 D 是 AC边的中点,以点 D 为顶点作∠FDE=120°,角的两边分别与直线 AB 和 BC 相交于点 F 和点 E
(1)试判断△ABC 的形状,说明理由
(2)如图 1,将△ABC 图形中∠FDE=120°绕顶点 D 旋转,当两边 DF、DE 分别与边 AB 和射线BC 相交于点 F、E 时,三线段 BE、BF、AB 之间存在什么关系?证明你的结论
(3)如图 2,当角两边 DF、DE 分别与射线 AB 和射线 BC 相交两点 F、E 时,三线段 BE、BF、AB 之间存在什么关系

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读材料.
点M,N在数轴上分别表示数m和n,我们把m,n之差的绝对值叫做点M,N之间的距离,即MN=|m﹣n|.如图,在数轴上,点A,B,O,C,D的位置如图所示,则DC=|3﹣1|=|2|=2;CO=|1﹣0|=|1|=1;BC=|(﹣2)﹣1|=|﹣3|=3;AB=|(﹣4)﹣(﹣2)|=|﹣2|=2.
![]()
(1)OA= ,BD= ;
(2)|1﹣(﹣4)|表示哪两点的距离?
(3)点P为数轴上一点,其表示的数为x,用含有x的式子表示BP= ,当BP=4时,x= ;当|x﹣3|+|x+2|的值最小时,x的取值范围是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
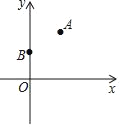
【题目】如图,在平面直角坐标系中,点A、B的坐标分别为(2,3)和(0,2).
(1)AB的长为 ;
(2)点C在y轴上,△ABC是等腰三角形,写出所有满足条件的点C的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com