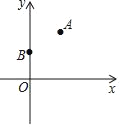
【题目】如图，在平面直角坐标系中，点A、B的坐标分别为（2，3）和（0，2）．
（1）AB的长为 ；
（2）点C在y轴上，△ABC是等腰三角形，写出所有满足条件的点C的坐标.
【答案】(1)
；（2）（0，4）或（0，2+）或（0，2﹣）或（0，
） ．
【解析】
（1）直接利用两点间的距离公式即可得出结论；
（2）分三种情况讨论，利用等腰三角形的性质建立方程求解即可．
（1）∵A（2，3），B（0，2），
∴AB=
，
故答案为；
（2）设点C（0，m），
∵A（2，3），B（0，2），
∴BC=|m-2|，AC=
，
由（1）知，AB=，
∵△ABC是等腰三角形，∴①当AB=AC时，
∴=，
∴m=2（舍）或m=4，
∴C（0，4），
②当AB=BC时，|m-2|=，
∴m=2±，
∴C（0，2+）或（0，2-），
③当AC=BC时，|m-2|=，
∴m=，
∴C（0，），
即：C（0，4）或（0，2+）或（0，2-）或（0，）．
故答案为：（0，4）或（0，2+）或（0，2-）或（0，）．
科目：初中数学 来源： 题型：
【题目】如图，正方形ABCD中，对角线AC、BD交于点O，将BD绕点B逆时针旋转30°到BE所在的位置，BE与AD交于点F，分别连接DE、CE．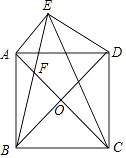
（1）求证：DE=DF；
（2）求证：AE∥BD；
（3）求tan∠ACE的值．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，在正三角形ABC中，D，E，F分别是BC，AC，AB上的点，DE⊥AC，EF⊥AB，FD⊥BC，则△DEF的面积与△ABC的面积之比等于（ ）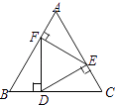 
A.1：3
B.2：3
C.
：2
D. ：3
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】利用等式的性质解下列方程：
(1)x－1＝3；
(2)－5x＝15；
(3)5x＋4＝－24；
(4)0.2x－0.5＝0.7；
(5)2x－1＝4x＋3；
(6)4－3x＝2x－1.
查看答案和解析>>
科目：初中数学 来源： 题型：
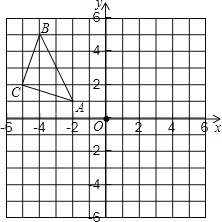
【题目】操作探究：如图，△ABC在平面直角坐标系中，其中，点A，B，C的坐标分别为A（–2，1），B（–4，5），C（–5，2）．
（1）作△ABC关于直线l：x=–1对称的△A1B1C1，其中，点A， B，C的对称点分别为点A1，B1，C1；
（2）写出点C1的坐标__________；
（3）在平面直角坐标系中有一点P位于第四象限，其坐标表示为P（m，n），则点P关于直线l的对称点Q的坐标表示为__________．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】已知∠AOB是一个直角，作射线OC，再分别作∠AOC和∠BOC的平分线OD，OE．
(1) 如图1，当∠BOC=70°时，求∠DOE的度数．
(2) 如图2，当射线OC在∠AOB内绕点O旋转时，∠DOE的大小是否发生变化?说明理由．
(3) 当射线OC在∠AOB外绕点O旋转且∠AOC为钝角时，画出图形，直接写出相应的∠DOE的度数．(不必写出过程)
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，点E、F、G、H分别是任意四边形ABCD中AD、BD、BC、CA的中点， 
（1）求证：四边形EFGH是平行四边形；
（2）四边形ABCD的边至少满足什么条件时，四边形EFGH是菱形？并说明理由．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，斜坡AB的坡度是i=1：2，坡角B处有一棵树BC，某一时刻测得树BC在斜坡AB上的影子BD的长度是10米，这时测得太阳光线与水平线的夹角为60°，则树BC的高度为多少米？（结果保留根号）．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
