
【题目】已知∠AOB是一个直角,作射线OC,再分别作∠AOC和∠BOC的平分线OD,OE.
(1) 如图1,当∠BOC=70°时,求∠DOE的度数.
(2) 如图2,当射线OC在∠AOB内绕点O旋转时,∠DOE的大小是否发生变化?说明理由.
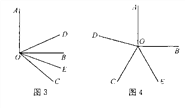
(3) 当射线OC在∠AOB外绕点O旋转且∠AOC为钝角时,画出图形,直接写出相应的∠DOE的度数.(不必写出过程)

【答案】(1)45°;(2)45°;(3) ∠DOE的大小发生变化.45°或135°.
【解析】试题分析:
(1)因为∠DOE=∠COD+∠COE,所以分别根据角平分线的定义求出∠COD和∠COE即可;
(2)因为∠DOE=∠COD+∠COE,结合角平分线即可求解;
(3)需要分类,当∠AOC是钝角时和当∠AOC大于钝角时,结合角平分线求解.
试题解析:
(1) 根据题意得∠AOC=90°-∠BOC=20°.因为OD,OE分别平分∠AOC和∠BOC,所以∠COD=![]() ∠AOC=10°,∠COE=
∠AOC=10°,∠COE=![]() ∠BOC=35°,所以∠DOE=∠COD+∠COE=45°
∠BOC=35°,所以∠DOE=∠COD+∠COE=45°
(2) ∠DOE的大小不变,理由:∠DOE=∠COD+∠COE=![]() ∠AOC+
∠AOC+![]() ∠COB=
∠COB=![]() (∠AOC+∠COB)=
(∠AOC+∠COB)= ![]() ∠AOB=45°
∠AOB=45°
(3) ∠DOE的大小发生变化.如图3,则∠DOE为45°;如图4,则∠DOE为135°


科目:初中数学 来源: 题型:
【题目】阅读材料.
点M,N在数轴上分别表示数m和n,我们把m,n之差的绝对值叫做点M,N之间的距离,即MN=|m﹣n|.如图,在数轴上,点A,B,O,C,D的位置如图所示,则DC=|3﹣1|=|2|=2;CO=|1﹣0|=|1|=1;BC=|(﹣2)﹣1|=|﹣3|=3;AB=|(﹣4)﹣(﹣2)|=|﹣2|=2.
![]()
(1)OA= ,BD= ;
(2)|1﹣(﹣4)|表示哪两点的距离?
(3)点P为数轴上一点,其表示的数为x,用含有x的式子表示BP= ,当BP=4时,x= ;当|x﹣3|+|x+2|的值最小时,x的取值范围是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对于实数a,我们规定:用符号[![]() ]表示不大于
]表示不大于![]() 的最大整数,称[
的最大整数,称[![]() ]为a的根整数,例如:[
]为a的根整数,例如:[![]() ]=3,[
]=3,[![]() ]=3.
]=3.
(1)仿照以上方法计算:[![]() ] = ;[
] = ;[![]() ] = .
] = .
(2)若[![]() ]=1,写出满足题意的x的整数值 .
]=1,写出满足题意的x的整数值 .
如果我们对a连续求根整数,直到结果为1为止.例如:对10连续求根整数2次 [![]() ]=3→[
]=3→[![]() ]=1,这时候结果为1.
]=1,这时候结果为1.
(3)对100连续求根整数, 次之后结果为1.
(4)只需进行3次连续求根整数运算后结果为1的所有正整数中,最大的是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
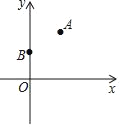
【题目】如图,在平面直角坐标系中,点A、B的坐标分别为(2,3)和(0,2).
(1)AB的长为 ;
(2)点C在y轴上,△ABC是等腰三角形,写出所有满足条件的点C的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】观察下列式子,并解决问题.
![]() ≈0.1260;
≈0.1260;![]() ≈0.2714;
≈0.2714;![]() ≈0.5848;
≈0.5848;![]() ≈1.260;
≈1.260;![]() ≈2.714.
≈2.714.
(1)![]() ≈ ,
≈ ,![]() ≈ ;
≈ ;
(2)若![]() ≈58.48,则x≈ ;
≈58.48,则x≈ ;
(3)通过类比,你能得到什么规律?用一句话描述出来.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明家与学校在同一直线上且相距720m,一天早上他和弟弟都匀速步行去上学,弟弟走得慢,先走1分钟后,小明才出发,已知小明的速度是80m/分,以小明出发开始计时,设时间为x(分),兄弟两人之间的距离为ym,图中的折线是y与x的函数关系的部分图象,根据图象解决下列问题:
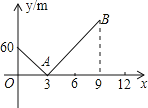
(1)弟弟步行的速度是 m/分,点B的坐标是 ;
(2)线段AB所表示的y与x的函数关系式是 ;
(3)试在图中补全点B以后的图象.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】正方形A1B1C1O,A2B2C2C1 , A3B3C3C2 , …按如图所示放置,点A1 , A2 , A3 , 和点C1 , C2 , C3 , …,分别在直线y=kx+b(k>0)和x轴上,已知点B1 , B2 , B3 , B4的坐标分别为(1,1)(3,2),(7,4),(15,8),则Bn的坐标是( ) 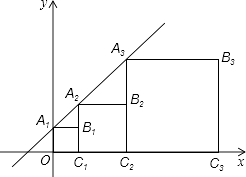
A.(2n﹣1,2n﹣1)
B.(2n , 2n﹣1)
C.(2n﹣1 , 2n)
D.(2n﹣1﹣1,2n﹣1)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com