【题目】观察下列式子,并解决问题.
≈0.1260;
≈0.2714;
≈0.5848;
≈1.260;
≈2.714.
(1)
≈ ,
≈ ;
(2)若
≈58.48,则x≈ ;
(3)通过类比,你能得到什么规律?用一句话描述出来.
【答案】答案见解析.
【解析】
（1）根据被开方数之间的1000倍关系得出结论；
（2）先找到与58.48有关的数，通过开立方的结果之间的关系，得出被开方数之间的关系；
（3）根据（1）（2）得出规律：被开方数的小数点每向右（左）移动3位，立方根的小数点向相同的方向移动1位．
（1）
=
=
×10≈0.5848×10=5.848；
=
=
×10≈1.260×10=12.60；
（2）∵≈0.5848，∴0.58483≈0.2．
∵
≈58.48，∴x=58.483=（0.5848×100）3=0.58483×1000000=0.2×1000000=200000；
（3）在开立方运算中，被开立方数的小数点向左或向右移动3n位时，其立方根的小数点相应地向左或向右移动n位(n为正整数)．
科目：初中数学 来源： 题型：
【题目】小伙李明刚多次将“宜昌柠檬”从宜昌市运往A市销售，市场调查发现：运往A市的火车与汽车的平均速度分别为100千米/时和80千米/时，运输费分别为每千米15m元和20m元，装卸费分别为2000m元和900m元（m为正数），火车、汽车装卸时间为2小时，运输过程中的损耗均为200m元/时．
（1）如果宜昌市与A市之间的路程400千米，求汽车的三费（装卸费、运输费、耗损费）比火车的三费多多少元？
（2）如果宜昌市与A市之间的路程为S千米，火车与汽车在运输途中停误的时间分别是2小时和3.1小时，请你通过计算说明，李明刚选择哪种方式比校合算．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】利用等式的性质解下列方程：
(1)x－1＝3；
(2)－5x＝15；
(3)5x＋4＝－24；
(4)0.2x－0.5＝0.7；
(5)2x－1＝4x＋3；
(6)4－3x＝2x－1.
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】已知∠AOB是一个直角，作射线OC，再分别作∠AOC和∠BOC的平分线OD，OE．
(1) 如图1，当∠BOC=70°时，求∠DOE的度数．
(2) 如图2，当射线OC在∠AOB内绕点O旋转时，∠DOE的大小是否发生变化?说明理由．
(3) 当射线OC在∠AOB外绕点O旋转且∠AOC为钝角时，画出图形，直接写出相应的∠DOE的度数．(不必写出过程)
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】某大型超市从生产基地购进一批水果,运输过程中质量损失10%.假设不计超市其他费用,如果超市要想获得至少20%的利润,那么这种水果的售价在进价基础上应至少提高( )
A. 
B. 
C. 
D. 
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，点E、F、G、H分别是任意四边形ABCD中AD、BD、BC、CA的中点， 
（1）求证：四边形EFGH是平行四边形；
（2）四边形ABCD的边至少满足什么条件时，四边形EFGH是菱形？并说明理由．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，已知△ABC中，AB=AC=10cm，BC=8cm，点D为AB的中点．
（1）如果点P在线段BC上以3cm/s的速度由B点向C点运动，同时，点Q在线段CA上由C点向A点运动．
①若点Q的运动速度与点P的运动速度相等，经过1s后，△BPD与△CQP是否全等，请说明理由；
②若点Q的运动速度与点P的运动速度不相等，当点Q的运动速度为多少时，能够使△BPD与△CQP全等？
（2）若点Q以②中的运动速度从点C出发，点P以原来的运动速度从点B同时出发，都逆时针沿△ABC三边运动，求经过多长时间点P与点Q第一次在△ABC的哪条边上相遇？
查看答案和解析>>
科目：初中数学 来源： 题型：
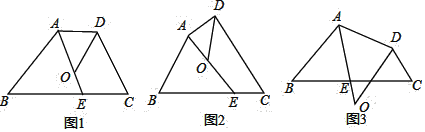
【题目】四边形ABCD中，∠BAD的角平分线与边BC交于点E，∠ADC的角平分线交直线AE于点O．
（1）若点O在四边形ABCD的内部，
①如图1，若AD∥BC，∠B=40°，∠C=70°，则∠DOE= °；
②如图2，试探索∠B、∠C、∠DOE之间的数量关系，并将你的探索过程写下来．
（2）如图3，若点O在四边形ABCD的外部，请你直接写出∠B、∠C、∠DOE之间的数量关系．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
