练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】下列四个图形中，既是轴对称又是中心对称的图形是（ ）
    A.4个
    B.3个
    C.2个
    D.1个

    【答案】C
    【解析】解：①是轴对称图形，也是中心对称图形，符合题意； ②是轴对称图形，不是中心对称图形，不符合题意；
    ③是轴对称图形，是中心对称图形，符合题意；
    ④轴对称图形，不是中心对称图形，不符合题意．
    综上可得①③符合题意．
    故选C．
    【考点精析】通过灵活运用轴对称图形和中心对称及中心对称图形，掌握两个完全一样的图形关于某条直线对折，如果两边能够完全重合，我们就说这两个图形成轴对称，这条直线就对称轴；如果把一个图形绕着某一点旋转180度后能与另一个图形重合，那么我们就说，这两个图形成中心对称；如果把一个图形绕着某一点旋转180度后能与自身重合，那么我们就说，这个图形成中心对称图形即可以解答此题．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】如图：二次函数y=ax2+bx+c的图象所示，下列结论中：①abc＞0；②2a+b=0；③当m≠1时，a+b＞am2+bm；④a﹣b+c＞0；⑤若ax12+bx1=ax22+bx2 ， 且x1≠x2 ， 则x1+x2=2，正确的个数为（ ）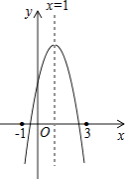
    A.1个
    B.2个
    C.3个
    D.4个

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，两条笔直的街道AB，CD相交于点O，街道OE，OF分别平分∠AOC，∠BOD，比较∠1与∠2的关系，并说明街道EOF是笔直的．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】操作探究：如图，△ABC在平面直角坐标系中，其中，点A，B，C的坐标分别为A（–2，1），B（–4，5），C（–5，2）．

    （1）作△ABC关于直线l：x=–1对称的△A1B1C1，其中，点A， B，C的对称点分别为点A1，B1，C1；

    （2）写出点C1的坐标__________；

    （3）在平面直角坐标系中有一点P位于第四象限，其坐标表示为P（m，n），则点P关于直线l的对称点Q的坐标表示为__________．

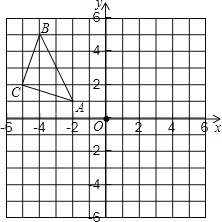
    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】某年级380名师生秋游，计划租用7辆客车，现有甲、乙两种型号客车，它们的载客量和租金如表．

    甲种客车

    乙种客车

    载客量（座/辆）

    60

    45

    租金（元/辆）

    550

    450

    （1）设租用甲种客车x辆，租车总费用为y元．求出y（元）与x（辆）之间的函数表达式；

    （2）当甲种客车有多少辆时，能保障所有的师生能参加秋游且租车费用最少，最少费用是多少元？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知∠AOB是一个直角，作射线OC，再分别作∠AOC和∠BOC的平分线OD，OE．

    (1) 如图1，当∠BOC=70°时，求∠DOE的度数．

    (2) 如图2，当射线OC在∠AOB内绕点O旋转时，∠DOE的大小是否发生变化?说明理由．

    (3) 当射线OC在∠AOB外绕点O旋转且∠AOC为钝角时，画出图形，直接写出相应的∠DOE的度数．(不必写出过程)

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，等边三角形ABC的边长为4，AD是BC边上的中线，F是AD边上的动点，E是AC边上一点．若AE＝2，当EF＋CF取得最小值时，∠ECF的度数为( )

    A. 20° B. 25° C. 30° D. 45°

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】在边长为1的小正方形网格中，△AOB的顶点均在格点上．

    （1）B点关于y轴的对称点坐标为 ；

    （2）将△AOB向左平移3个单位长度，再向上平移2个单位长度得到△A1O1B1，请画出△A1O1B1；

    （3）在（2）的条件下，△AOB边AB上有一点P的坐标为（a，b），则平移后对应点P1的坐标为 ．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，直线y=﹣x+3与x轴，y轴分别交于B，C两点，抛物线y=ax2+bx+c过A（1，0），B，C三点．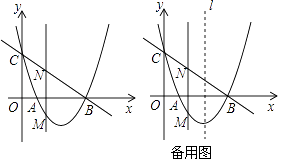

    （1）求抛物线的解析式；
    （2）若点M是抛物线在x轴下方图形上的动点，过点M作MN∥y轴交直线BC于点N，求线段MN的最大值．
    （3）在（2）的条件下，当MN取得最大值时，在抛物线的对称轴l上是否存在点P，使△PBN是以BN为腰的等腰三角形？若存在，求出点P的坐标，若不存在，请说明理由．

    查看答案和解析>>

    同步练习册答案