
如图,在矩形ABCD中,AB=20cm,BC=4cm,点p从A开始折线A——B——C——D以4cm/秒的 速度 移动,点Q从C开始沿CD边以1cm/秒的速度移动,如果点P、Q分别从A、C同时出发,当其中一点到达D时,另一点也随之停止运动,设运动的时间t(秒)
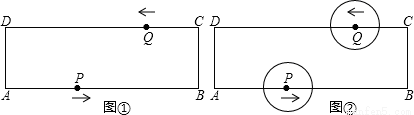
(1)t为何值时,四边形APQD为矩形.
(2)如图(2),如果⊙P和⊙Q的半径都是2cm,那么t为何值时,⊙P和⊙Q外切?
(1)4;(2)t为4s,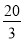 s,
s,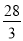 s时,⊙P与⊙Q外切.
s时,⊙P与⊙Q外切.
【解析】
试题分析:(1)四边形APQD为矩形,也就是AP=DQ,分别用含t的代数式表示,解即可;
(2)主要考虑有四种情况,一种是P在AB上,一种是P在BC上时.一种是P在CD上时,又分为两种情况,一种是P在Q右侧,一种是P在Q左侧.并根据每一种情况,找出相等关系,解即可.
试题解析:(1)根据题意,当AP=DQ时,四边形APQD为矩形.此时,4t=20-t,解得t=4(s).
答:t为4时,四边形APQD为矩形
(2)当PQ=4时,⊙P与⊙Q外切.
①如果点P在AB上运动.只有当四边形APQD为矩形时,PQ=4.由(1),得t=4(s);
②如果点P在BC上运动.此时t≥5,则CQ≥5,PQ≥CQ≥5>4,∴⊙P与⊙Q外离;
③如果点P在CD上运动,且点P在点Q的右侧.可得CQ=t,CP=4t-24.当CQ-CP=4时,⊙P与⊙Q外切.此时,t-(4t-24)=4,解得t=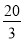 (s);
(s);
④如果点P在CD上运动,且点P在点Q的左侧.当CP-CQ=4时,⊙P与⊙Q外切.此时,4t-24-t=4,
解得t=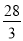 (s),
(s),
∵点P从A开始沿折线A-B-C-D移动到D需要11s,点Q从C开始沿CD边移动到D需要20s,而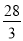 <11,
<11,
∴当t为4s,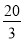 s,
s,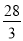 s时,⊙P与⊙Q外切.
s时,⊙P与⊙Q外切.
考点:1.矩形的性质;2.圆与圆的位置关系.


 53随堂测系列答案
53随堂测系列答案科目:初中数学 来源:2014年青岛版初中数学九年级下册第八章8.2盲区练习卷(解析版) 题型:选择题
当你站在博物馆的展览厅中时,你知道站在何处观赏最理想吗?如图,设墙壁上的展品最高点P距地面2.5米,最低点Q距地面2米,观赏者的眼睛F距地面1.6米,当视角∠PEQ最大时,站在此处观赏最理想,则此时E到墙壁的距离为( )米.

A.1 B.0.6 C.0.5 D.0.4
查看答案和解析>>
科目:初中数学 来源:2014-2015学年河北省九年级上学期第二次月考数学试卷(解析版) 题型:选择题
将抛物线 的顶点向左平移
的顶点向左平移 个单位长度,所得到的点的坐标是( )
个单位长度,所得到的点的坐标是( )
A.( ,0) B.(0,
,0) B.(0, ) C.(0,
) C.(0, ) D.(
) D.( ,0)
,0)
查看答案和解析>>
科目:初中数学 来源:2013-2014学年黑龙江省牡丹江管理局北斗星协会九年级中考三模数学试卷(解析版) 题型:解答题
(本题满分8分)B岛位于自然环境优美的西沙群岛,盛产多种鱼类。A港、B岛、C港依次在同一条直线上,一渔船从A港出发经由B岛向C港航行,航行2小时时发现鱼群,于是渔船匀速缓慢向B港方向前行打渔。在渔船出发一小时后,一艘快艇由C港出发,经由B岛前往A港运送物资。当快艇到达B岛时渔船恰好打渔结束,渔船又以原速经由B岛到达C港。下面是两船距B港的距离y(海里)与渔船航行时间x(小时)的函数图象,结合图象回答下列问题:
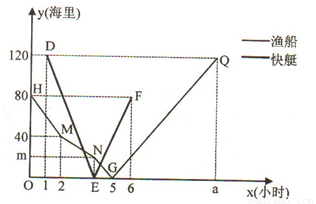
(1)请直接写出m,a的值.
(2)求出线段MN的解析式,并写出自变量的取值范围。
(3)从渔船出发后第几小时两船相距10海里?
查看答案和解析>>
科目:初中数学 来源:2013-2014学年河北省九年级上学期期末考试数学试卷(解析版) 题型:选择题
下图为二次函数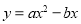 的图像,若一元二次方程
的图像,若一元二次方程 有实数根,则m的最小值为( )
有实数根,则m的最小值为( )

A.8 B.4 C.-4 D.-8
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com