
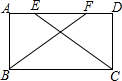
 已知,如图,在矩形ABCD中,点E,F在边AD上,且AE=DF,求证:BF=CE.
已知,如图,在矩形ABCD中,点E,F在边AD上,且AE=DF,求证:BF=CE. 科目:初中数学 来源: 题型:选择题
| A. | 165 | B. | 168 | C. | 170 | D. | 172 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
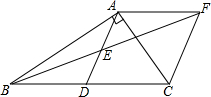 在Rt△ABC中,∠BAC=90°,D是BC的中点,E是AD的中点,过点A作AF∥BC交BE的延长线于点F.
在Rt△ABC中,∠BAC=90°,D是BC的中点,E是AD的中点,过点A作AF∥BC交BE的延长线于点F.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
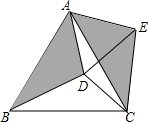 如图,在等边△ABC内有一点D,AD=5,BD=6,CD=4,将△ABD绕A点逆时针旋转,使AB与AC重合,点D旋转至点E,则∠CDE的正切值为3$\sqrt{7}$.
如图,在等边△ABC内有一点D,AD=5,BD=6,CD=4,将△ABD绕A点逆时针旋转,使AB与AC重合,点D旋转至点E,则∠CDE的正切值为3$\sqrt{7}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 两人相遇次数 (单位:次) | 1 | 2 | 3 | 4 | … | n |
| 两人所跑路程之和 (单位:m) | 100 | 300 | 500 | 700 | … | 200n-100 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
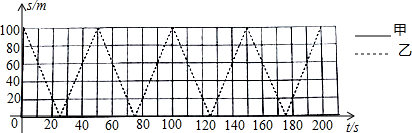
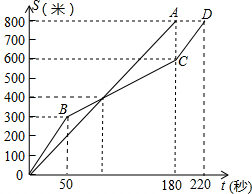 在一次800米的长跑比赛中,甲、乙两人所跑的路程s(米)与各自所用时间t(秒)之间的函数图象分别为线段OA和折线OBCD,则下列说法正确的是( )
在一次800米的长跑比赛中,甲、乙两人所跑的路程s(米)与各自所用时间t(秒)之间的函数图象分别为线段OA和折线OBCD,则下列说法正确的是( )| A. | 甲的速度随时间的增加而增大 | B. | 乙的平均速度比甲的平均速度大 | ||
| C. | 在起跑后第180秒时,两人相遇 | D. | 在起跑后第50秒时,乙在甲的前面 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com