
【题目】(本小题满分11分)已知∠ABC=90°,D是直线AB上的点,AD=BC.
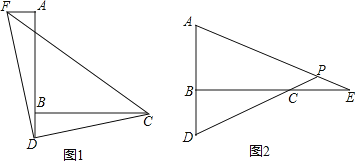
(1)如图1,过点A作AF⊥AB,并截取AF=BD,连接DC、DF、CF,判断△CDF的形状并证明;
(2)如图2,E是直线BC上一点,且CE=BD,直线AE、CD相交于点P,∠APD的度数是一个固定的值吗?若是,请求出它的度数;若不是,请说明理由.
【答案】见解析
【解析】(1)△CDF是等腰直角三角形,(1分)
理由如下:
∵AF⊥AD,∠ABC=90°,∴∠FAD=∠DBC,(2分)
在△FAD与△DBC中,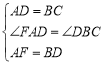 ,∴△FAD≌△DBC(SAS),(3分)
,∴△FAD≌△DBC(SAS),(3分)
∴FD=DC,∴△CDF是等腰三角形,(4分)
∵△FAD≌△DBC,∴∠FDA=∠DCB,
∵∠BDC+∠DCB=90°,∴∠BDC+∠FDA=90°,∴△CDF是等腰直角三角形.(5分)
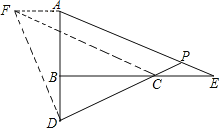
(2)作AF⊥AB于A,使AF=BD,连接DF,CF,如图,
∵AF⊥AD,∠ABC=90°,∴∠FAD=∠DBC,
在△FAD与△DBC中,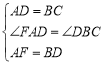 ,
,
∴△FAD≌△DBC(SAS),∴FD=DC,∴△CDF是等腰三角形,(6分)
∵△FAD≌△DBC,∴∠FDA=∠DCB,
∵∠BDC+∠DCB=90°,∴∠BDC+∠FDA=90°,
∴△CDF是等腰直角三角形,(7分)
∴∠FCD=45°,(8分)
∵AF∥CE,且AF=CE,∴四边形AFCE是平行四边形,(10分)
∴AE∥CF,∴∠APD=∠FCD=45°.(11分)


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
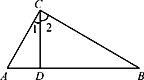
【题目】如图,在△ABC中,∠ACB=90°,CD是高.
(1)图中有几个直角三角形?是哪几个?
(2)∠1和∠A有什么关系?∠2和∠A呢?还有哪些锐角相等.
查看答案和解析>>
科目:初中数学 来源: 题型:
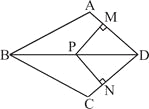
【题目】在四边形ABCD中,AB=BC,对角线BD平分![]() ,P是BD上一点,过P作PM⊥AD于点M,PN⊥CD于点N.
,P是BD上一点,过P作PM⊥AD于点M,PN⊥CD于点N.
(1)求证: ![]() ;
;
(2)若![]() ,求证:四边形MPND是正方形。
,求证:四边形MPND是正方形。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(本题12分)若点A、B在数轴上分别表示实数a、b,则我们可以定义|a-b|为A、B两点之间的距离,表示为|AB|=|a-b|.根据这个定义回答下列问题:
(1)数轴上表示2和5的两点之间的距离是______ ,表示-2和-5的两点之间的距离是______ ;表示1和-3的两点之间的距离是______ ;表示x和-1的两点A和B之间的距离是_____ ;
(2)如果|x+3|=2,求![]() 的值;
的值;
(3)代数式|x+3|+|x-2|最小值是______ ;方程|x+3|+|x-2|=7的解为 。
查看答案和解析>>
科目:初中数学 来源: 题型:
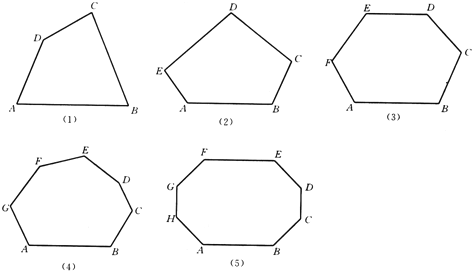
【题目】分别画出下列各多边形的对角线,并观察图形完成下列问题:
(1)试写出用n边形的边数n表示对角线总条数S的式子: .
(2)从十五边形的一个顶点可以引出 条对角线,十五边形共有 条对角线:
(3)如果一个多边形对角线的条数与它的边数相等,求这个多边形的边数.
查看答案和解析>>
科目:初中数学 来源: 题型:
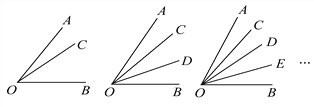
【题目】如图,在锐角∠AOB内部画1条射线,可得3个锐角,画2条不同的射线,可得6个锐角,画3条不同的射线,可得10个锐角……照此规律,画10条不同的射线,可得锐角多少个?
查看答案和解析>>
科目:初中数学 来源: 题型:
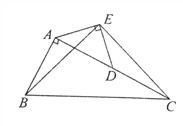
【题目】如图在Rt△ABC中,∠BAC=90 o,AC=2AB,点D是AC的中点,将一块锐角为45 o的直角三角板如图放置,使三角板斜边的两个端点分别与A,D重合,连接BE,EC。试猜想线段BE和EC的数量及位置关系,并证明你的猜想。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】关于x的一元二次方程x2+2x+2m=0有两个不相等的实数根.
(1)求m的取值范围;
(2)若x1,x2是一元二次方程x2+2x+2m=0的两个根,且x12+x22=8,求m的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com