
在直角坐标系中,O为坐标原点,点A的坐标为(2,2),点C是线段OA上的一个动点(不运动至O,A两点),过点C作CD⊥x轴,垂足为D,以CD为边在右侧作正方形CDEF. 连接AF并延长交x轴的正半轴于点B,连接OF,设OD=t.
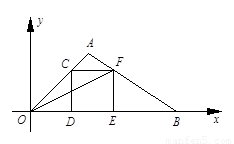
⑴ 求tan∠FOB的值;
⑵用含t的代数式表示△OAB的面积S;
⑶是否存在点C, 使以B,E,F为顶点的三角形与△OFE相似,若存在,请求出所有满足要求的B点的坐标;若不存在,请说明理由.
⑴1/2⑵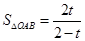 ⑶(6,0),(1,0),(3,0)
⑶(6,0),(1,0),(3,0)
【解析】(1)∵A(2,2) ∴∠AOB=45°
∴CD=OD=DE=EF=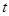 ∴
∴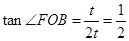 ……………………(2分)
……………………(2分)
(2)由△ACF~△AOB得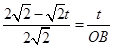
∴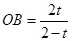 ∴
∴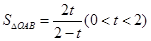 ……………………(4分)
……………………(4分)
(3)要使△BEF与△OFE相似,∵∠FEO=∠FEB=90°
∴只要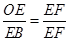 或
或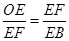
即: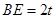 或
或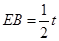
①当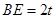 时,
时, 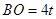 ,
,
∴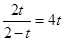 ∴
∴ (舍去)或
(舍去)或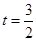 ∴B(6,0) …………………(2分)
∴B(6,0) …………………(2分)
②当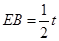 时,
时,
(ⅰ)当B在E的左侧时,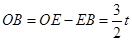 ,
,
∴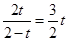 ∴
∴ (舍去)或
(舍去)或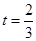 ∴B(1,0) ……………(2分)
∴B(1,0) ……………(2分)
(ⅱ)当B在E的右侧时,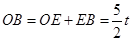 ,
,
∴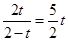 ∴
∴ (舍去)或
(舍去)或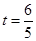 ∴B(3,0) ……………(2分)
∴B(3,0) ……………(2分)
(1)已知点A的坐标,可推出CD=OD=DE=EF=t,可求出tan∠FOB.
(2)证明△ACF∽△AOB推出得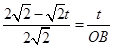 ,然后求出OB关于t的等量关系式,继而求出S△OAB的值.
,然后求出OB关于t的等量关系式,继而求出S△OAB的值.
(3)依题意要使△BEF∽△OFE,则要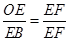 或
或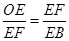 ,即分BE=2t或
,即分BE=2t或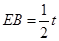 两种情况解答.当BE=2t时,BO=4t,根据上述的线段比求出t值;当
两种情况解答.当BE=2t时,BO=4t,根据上述的线段比求出t值;当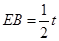 时也要细分两种情况:当B在E的右侧以及当B在E的左侧时OB的取值,利用线段比求出t值.
时也要细分两种情况:当B在E的右侧以及当B在E的左侧时OB的取值,利用线段比求出t值.


科目:初中数学 来源: 题型:
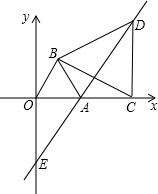 OAB,C为x轴正半轴上的一个动点(OC>1),连接BC,以BC为边在第一象限内作等边△BCD,直线DA交y轴于E点.
OAB,C为x轴正半轴上的一个动点(OC>1),连接BC,以BC为边在第一象限内作等边△BCD,直线DA交y轴于E点.查看答案和解析>>
科目:初中数学 来源: 题型:
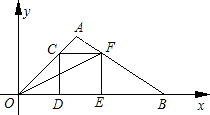 在直角坐标系中,O为坐标原点,点A的坐标为(2,2),点C是线段OA上的一个动点(不运动至O,A两点),过点C作CD⊥x轴,垂足为D,以CD为边在右侧作正方形CDEF.连接AF并延长交x轴的正半轴于点B,连接OF,设OD=t.
在直角坐标系中,O为坐标原点,点A的坐标为(2,2),点C是线段OA上的一个动点(不运动至O,A两点),过点C作CD⊥x轴,垂足为D,以CD为边在右侧作正方形CDEF.连接AF并延长交x轴的正半轴于点B,连接OF,设OD=t.查看答案和解析>>
科目:初中数学 来源: 题型:
| 4 | 3 |
 点B′处,C的对应点为C′.
点B′处,C的对应点为C′.查看答案和解析>>
科目:初中数学 来源: 题型:
| 3 |
| 3 |
| 3 |
| 3 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com