
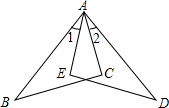
 如图,已知AB=AD,∠B=∠D,∠1=∠2,说明:BC=DE.
如图,已知AB=AD,∠B=∠D,∠1=∠2,说明:BC=DE.科目:初中数学 来源: 题型:
 如图,在以O为原点的直角坐标系中,点A、C分别在x轴、y轴的正半轴上,点B在第一象限,四边形OABC是矩形,OA=8,OC=6.反比例函数y1=
如图,在以O为原点的直角坐标系中,点A、C分别在x轴、y轴的正半轴上,点B在第一象限,四边形OABC是矩形,OA=8,OC=6.反比例函数y1=| k |
| x |
| k |
| x |
查看答案和解析>>
科目:初中数学 来源: 题型:
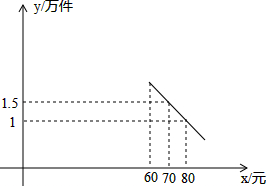 某企业在自主研制新产品的同时考虑招聘员工的计划,已知该产品的生产成本为每件40元,员工每人每月的工资为2500元,公司每月需支付其他费用15万元,设产品月销售量为y(万件),销售单价为x(元),试销阶段40≤x≤60,企业把试销情况列成表格(见下表),正式销售阶段60<x<100,企业把销售情况绘制成函数关系(见下图).
某企业在自主研制新产品的同时考虑招聘员工的计划,已知该产品的生产成本为每件40元,员工每人每月的工资为2500元,公司每月需支付其他费用15万元,设产品月销售量为y(万件),销售单价为x(元),试销阶段40≤x≤60,企业把试销情况列成表格(见下表),正式销售阶段60<x<100,企业把销售情况绘制成函数关系(见下图).
| 月销售量y/万件 | 4 | 3.5 | 2 | |
| 销售单价x/元 | 40 | 45 | 60 |
查看答案和解析>>
科目:初中数学 来源: 题型:

查看答案和解析>>
科目:初中数学 来源: 题型:
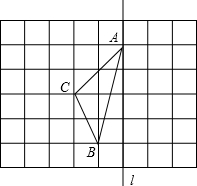 如图,在长度为1个单位长度的小正方形组成的正方形网格中,点A、B、C在小正方形的顶点上.
如图,在长度为1个单位长度的小正方形组成的正方形网格中,点A、B、C在小正方形的顶点上.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com