
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |


 单元加期末复习先锋大考卷系列答案
单元加期末复习先锋大考卷系列答案 出彩同步大试卷系列答案
出彩同步大试卷系列答案科目:初中数学 来源: 题型:
| A、平均数 | B、众数 |
| C、中位数 | D、方差 |
查看答案和解析>>
科目:初中数学 来源: 题型:
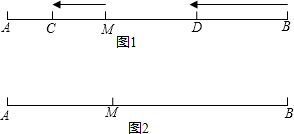 如图①,已知点M是线段AB上一点,点C在线段AM上,点D在线段BM上,C、D两点分别从M、B出发以1cm/s、3cm/s的速度沿直线BA向左运动,运动方向如箭头所示.
如图①,已知点M是线段AB上一点,点C在线段AM上,点D在线段BM上,C、D两点分别从M、B出发以1cm/s、3cm/s的速度沿直线BA向左运动,运动方向如箭头所示.| 1 |
| 4 |
| MN |
| AB |
查看答案和解析>>
科目:初中数学 来源: 题型:
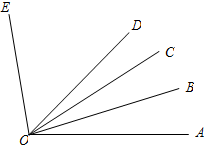 已知∠AOB=20°,∠AOE=100°,OB平分∠AOC,OD平分∠AOE.
已知∠AOB=20°,∠AOE=100°,OB平分∠AOC,OD平分∠AOE.查看答案和解析>>
科目:初中数学 来源: 题型:
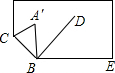 如图所示,将一长方形纸的一角斜折过去,使顶点A落在A′处,BC为折痕,如果BD为∠A′BE的平分线,则∠CBD=( )
如图所示,将一长方形纸的一角斜折过去,使顶点A落在A′处,BC为折痕,如果BD为∠A′BE的平分线,则∠CBD=( )| A、90° | B、80° |
| C、100° | D、70° |
查看答案和解析>>
科目:初中数学 来源: 题型:
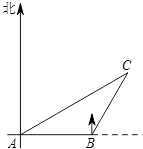 如图,一艘渔船正自西向东航行追赶鱼群,在A处望见岛C在船的北偏东60°方向,前进20海里到达B处,此时望见岛C在船的北偏东30°方向,以岛C为中心的12海里内为军事演习的危险区.请通过计算说明:如果这艘渔船继续向东追赶鱼群是否有进入危险区的可能.(参考数据:
如图,一艘渔船正自西向东航行追赶鱼群,在A处望见岛C在船的北偏东60°方向,前进20海里到达B处,此时望见岛C在船的北偏东30°方向,以岛C为中心的12海里内为军事演习的危险区.请通过计算说明:如果这艘渔船继续向东追赶鱼群是否有进入危险区的可能.(参考数据:| 2 |
| 3 |
查看答案和解析>>
科目:初中数学 来源: 题型:
 二次函数y=ax2+bx+c的图象如图所示,那么关于x的方程ax2+bx+c=0的根的情况是( )
二次函数y=ax2+bx+c的图象如图所示,那么关于x的方程ax2+bx+c=0的根的情况是( )| A、有两个不相等的实数根 |
| B、有两个异号实数根 |
| C、有两个相等的实数根 |
| D、无实数根 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com