解:(1)PA的长度为:10-t,
QE=PQ.
(2)四边形EBPA的面积不会变化.
∵BF∥AC,
∴BF与AC的距离处处相等.
设EF与AC的距离为h,
又∵PE∥BC,
∴四边形EBCP是平行四边形.
∴EB=PC=t,AP=10-t,
∴S
四边形EBPA=

(EB+AP)h=

(t+10-t)•h=5h;
(3)①AQ=t,则BQ=10-t,
又∵AP=10-t,EB=t,
∴EB=AQ,BQ=AP,
又∵BF∥AC,
∴∠EBA=∠QAP,
∴△EBQ≌△QAP,
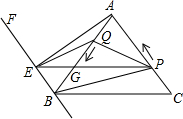
在△ABC中,AB=AC=10cm,BC=12cm,作AH⊥BC于H,
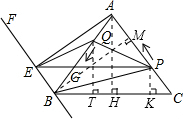
则CH=

BC=

×12=6,
AH=

=

=8,
作BM⊥AC于点M,
∵S
△ABC=

•BC•AH=

•AC•BM,
∴12×8=10•BM
BM=

,
∴S
△ABP=

(10-t)×

,
即S=48-

t.
②
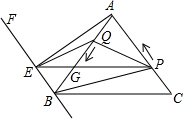
∵BF∥AC,∴BE不平行于PQ,
∴当EQ∥BP时,四边形EBPQ是梯形.
∴∠GEQ=∠GPB,∠EQB=∠GBP,
∴△EGQ∽△PGB,
∴
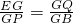
,
又∵AB=AC,
∴∠ABC=∠C.
又∵PG∥BC,且PG≠BC,
∴四边形GBCP是等腰梯形,
∴GB=PC=t,
∴GQ=10-2t,
同理可证△AGP∽△EGB,
∴
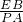
=
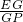
∴
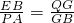
,
∴
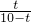
=
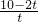
,
化简得:t
2-30t+100=0,
解得:t
1=15+5

(舍去),t
2=15-5

,
当t=15-5

是,四边形EBPQ是梯形.
分析:(1)因为AC=10cm,点P以以1cm/s的速度从A出发,从而可得出代数式,线段QE和QP相等.
(2)四边形EBPA的面积不会变化,可求出四边形的面积.
(3)根据三角形全等和勾股定理,以及三角形的面积表示出四边形的面积求出解以及根据梯形的概念判断出梯形.
点评:本题考查平行四边形的判定和性质,全等三角形的判定和性质,梯形的概念等知识点.

 用“>、<、=、≥、≤”符号表示);
用“>、<、=、≥、≤”符号表示); (EB+AP)h=
(EB+AP)h= (t+10-t)•h=5h;
(t+10-t)•h=5h;
 BC=
BC= ×12=6,
×12=6, =
= =8,
=8, •BC•AH=
•BC•AH= •AC•BM,
•AC•BM, ,
, (10-t)×
(10-t)× ,
, t.
t. ∵BF∥AC,∴BE不平行于PQ,
∵BF∥AC,∴BE不平行于PQ,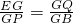 ,
,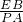 =
=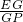 ∴
∴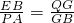 ,
,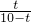 =
=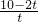 ,
, (舍去),t2=15-5
(舍去),t2=15-5 ,
, 是,四边形EBPQ是梯形.
是,四边形EBPQ是梯形.

 24、如图,AB=AC=AD.
24、如图,AB=AC=AD.