Question

7．如图，在平面直角坐标系中，四边形OADC是矩形，OA=6，AB=4，直线y=-x+3与坐标轴交于D，E．设M是AB的中点，P是线段DE上的动点，
（1）求M、D两点的坐标；
（2）当P在什么位置时，PA=PB求出此时P点的坐标；
（3）过P作PH⊥BC，垂足为H，当以PM为直径的⊙F与BC相切于点N时，求梯形PMBH的面积．

Answer 1

分析 （1）因为四边形OABC是矩形，OA=6，AB=4，直线3与坐标轴交于D、E，M是AB的中点，求出M的坐标；令y=0，即可求出D的坐标；
（2）由题意得出P是AB的垂直平分线和直线ED的交点，而AB的中垂线是y=2，得P的纵坐标为2，令直线ED的解析式中的y=2，求出的x的值即可；
（3）可设P（x，y），连接PN、MN、NF，因为点P在y=-x+3上，所以P（x，-x+3），根据题意可得PN⊥MN，FN⊥BC，F是圆心，又因N是线段HB的中点，HN=NB=$\frac{6-x}{2}$，PH=4-（-x+3）=x+1，BM=2，利用直径对的圆周角是直角可得到∠HPN+∠HNP=∠HNP+∠BNM=90°，得出∠HPN=∠BNM，证出△PNH∽△NMB，得出对应边成比例，得到关于x的方程，解之即可求出x的值，即可求出梯形的面积．

解答 解：（1）∵四边形OABC是矩形，OA=6，AB=4，M是AB的中点，
∴OA=6，AM=BM=2，
∴M（6，2）；
∵直线y=-x+3与坐标轴交于D，E，
∴当y=0时，-x+3=0，
解得：x=3，
∴D（3，0）；

（2）∵PA=PB，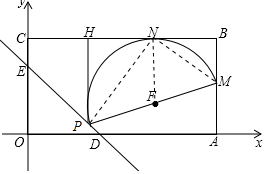
∴点P在线段AB的中垂线上，
∴点P的纵坐标是2，
又∵点P在y=-x+3上，
∴2=-x+3，
∴x=1，
∴点P的坐标为（ 1，2）；

（3）设P（x，y），连接PN、MN、NF，如图所示：
∵点P在y=-x+3上，
∴P（x，-x+3），
依题意知：PN⊥MN，FN⊥BC，F是圆心，
∴N是线段HB的中点，HN=NB=$\frac{6-x}{2}$，PH=4-（-x+3）=x+1，BM=2，
∵∠HPN+∠HNP=∠HNP+∠BNM=90°，
∴∠HPN=∠BNM，
又∵∠PHN=∠B=90°，
∴Rt△PNH∽Rt△NMB，
∴$\frac{HN}{BM}=\frac{PH}{BN}$，
∴$\frac{\frac{6-x}{2}}{2}=\frac{x+1}{\frac{6-x}{2}}$，
整理得：x²-20x+28=0，
解得：x=10+6$\sqrt{2}$（不合题意，舍去），或x=10-6$\sqrt{2}$，
∴梯形PMBH的面积=$\frac{1}{2}$（BM+PH）•BH=$\frac{1}{2}$（2+10-6$\sqrt{2}$+1）（6-10+6$\sqrt{2}$）=51$\sqrt{2}$-62．

点评 本题是圆的综合题目题目，考查了矩形的性质、坐标与图形性质、一次函数的应用、相似三角形的判定与性质、一元二次方程的解法以及梯形面积的计算方法等知识；本题综合性强，有一定难度．