
分析 (1)首先把二次项系数化为1,然后进行配方,最后开方解方程;
(2)先把x2-6x+9=(5-2x)2化为(x-3)2=(5-2x)2,然后利用平方差公式分解因式得到(2-x)(3x-8)=0,最后解一元一次方程即可.
解答 解:(1)∵6x2-x-12=0,
∴x2-$\frac{1}{6}$x=2,
∴(x-$\frac{1}{12}$)2=$\frac{287}{144}$,
∴x-$\frac{1}{12}$=±$\frac{\sqrt{287}}{12}$,
∴x1=$\frac{1+\sqrt{287}}{12}$,x2=$\frac{1-\sqrt{287}}{12}$;
(2)∵x2-6x+9=(5-2x)2,
∴(x-3)2=(5-2x)2,
∴(x-3)2-(5-2x)2=0,
∴(x-3+5-2x)(x-3-5+2x)=0,
∴(2-x)(3x-8)=0,
∴x1=2,x2=$\frac{8}{3}$.
点评 本题主要考查了因式分解法以及配方法解一元二次方程的知识,解答本题的关键是熟练掌握因式分解法和配方法解方程的步骤,此题难度一般.


 全程金卷系列答案
全程金卷系列答案 快乐5加2金卷系列答案
快乐5加2金卷系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
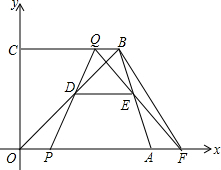 如图,在直角梯形OABC中,OA∥CB,A、B两点的坐标分别为A(15,0),B(10,12),动点P、Q分别从O、B出发,点P以每秒2个单位长度的速度沿OA向终点A运动,点Q以每秒1个单位的速度沿BC向终点C运动,当点P停止运动时,点Q也同时停止运动.线段OB、PQ相交于点D,过点D作DE∥OA,交AB于点E,连接QE并延长,交x轴于点F.设动点P、Q的运动时间为t(单位:秒)
如图,在直角梯形OABC中,OA∥CB,A、B两点的坐标分别为A(15,0),B(10,12),动点P、Q分别从O、B出发,点P以每秒2个单位长度的速度沿OA向终点A运动,点Q以每秒1个单位的速度沿BC向终点C运动,当点P停止运动时,点Q也同时停止运动.线段OB、PQ相交于点D,过点D作DE∥OA,交AB于点E,连接QE并延长,交x轴于点F.设动点P、Q的运动时间为t(单位:秒)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 在四边形ABCD中,E、F、G、H分别是AB、BC、CD、DA边上的中点,阅读下列材料,回答问题:
在四边形ABCD中,E、F、G、H分别是AB、BC、CD、DA边上的中点,阅读下列材料,回答问题:查看答案和解析>>
科目:初中数学 来源: 题型:填空题
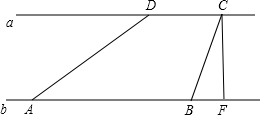 如图,河流两岸a、b平行,C、D是河岸a上间隔50米的两根电线杆,某人在河岸b上的A处测得∠DAE=30°,然后沿河岸走了100米到达B处,测得∠CBF=60°,则河流的宽度CF的值为43m(结果精确到个位,$\sqrt{2}$≈1.414,$\sqrt{3}$≈1.732)
如图,河流两岸a、b平行,C、D是河岸a上间隔50米的两根电线杆,某人在河岸b上的A处测得∠DAE=30°,然后沿河岸走了100米到达B处,测得∠CBF=60°,则河流的宽度CF的值为43m(结果精确到个位,$\sqrt{2}$≈1.414,$\sqrt{3}$≈1.732)查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com