
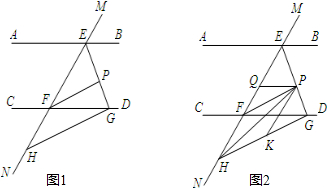
分析 (1)利用平行线的性质推知∠BEF+∠EFD=180°;然后根据角平分线的性质、三角形内角和定理证得∠EPF=90°,即EG⊥PF,故结合已知条件GH⊥EG,易证PF∥GH;
(2)利用三角形外角定理、三角形内角和定理求得∠4=90°-∠3=90°-2∠2;然后由邻补角的定义、角平分线的定义推知∠QPK=$\frac{1}{2}$∠EPK=45°+∠2;最后根据图形中的角与角间的和差关系求得∠HPQ的大小不变,是定值45°.
解答 (1)证明:如图1,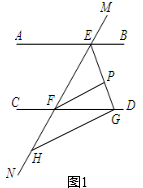
∵AB∥CD,
∴∠BEF+∠EFD=180°.
又∵∠BEF与∠EFD的角平分线交于点P,
∴∠FEP+∠EFP=$\frac{1}{2}$(∠BEF+∠EFD)=90°,
∴∠EPF=90°,即EG⊥PF.
∵GH⊥EG,
∴PF∥GH;
(2)解:∠HPQ的大小不发生变化,理由如下: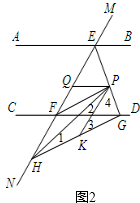
如图2,∵∠1=∠2,
∴∠3=2∠2.
又∵GH⊥EG,
∴∠4=90°-∠3=90°-2∠2.
∴∠EPK=180°-∠4=90°+2∠2.
∵PQ平分∠EPK,
∴∠QPK=$\frac{1}{2}$∠EPK=45°+∠2.
∴∠HPQ=∠QPK-∠2=45°,
∴∠HPQ的大小不发生变化,一直是45°.
点评 本题主要考查平行线的性质和判定,掌握平行线的性质和判定是解题的关键,即①两直线平行?同位角相等,②两直线平行?内错角相等,③两直线平行?同旁内角互补,④a∥b,b∥c⇒a∥c.


 世纪百通主体课堂小学课时同步达标系列答案
世纪百通主体课堂小学课时同步达标系列答案 世纪百通优练测系列答案
世纪百通优练测系列答案科目:初中数学 来源: 题型:解答题
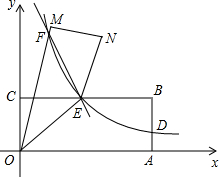 如图,矩形OABC在第一象限,OA=a,OC=b,双曲线y=$\frac{k}{x}$(x>0)始终经过BC的中点E,且与AB交于点D,连接OE.
如图,矩形OABC在第一象限,OA=a,OC=b,双曲线y=$\frac{k}{x}$(x>0)始终经过BC的中点E,且与AB交于点D,连接OE.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
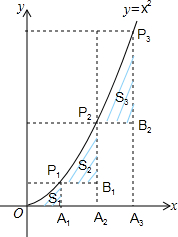 如图,已知A1,A2,A3,…,A2014是x轴上的点,且0A1=A1A2=A2A3=…=A2013A2014=A2013A2014=1,分别过点A1,A2,A3,…,A2014作x轴的垂线交二次函数y=x2(x≥0)的图象于点P1,P2,P3,…,P2014.若△OA1P1的面积为S1,过点P1作P1B1⊥A2P2于点B1,记△P1B1P2的面积为S2,过点P2作P2B2⊥A3P3于点B2,记△P2B2P3的面积为S3,…依次进行下去,最后记△P2013B2013P2014的面积为S2014,则S3=$\frac{5}{2}$,S2014-S2013=1.
如图,已知A1,A2,A3,…,A2014是x轴上的点,且0A1=A1A2=A2A3=…=A2013A2014=A2013A2014=1,分别过点A1,A2,A3,…,A2014作x轴的垂线交二次函数y=x2(x≥0)的图象于点P1,P2,P3,…,P2014.若△OA1P1的面积为S1,过点P1作P1B1⊥A2P2于点B1,记△P1B1P2的面积为S2,过点P2作P2B2⊥A3P3于点B2,记△P2B2P3的面积为S3,…依次进行下去,最后记△P2013B2013P2014的面积为S2014,则S3=$\frac{5}{2}$,S2014-S2013=1.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\sqrt{\frac{1}{3}}$ | B. | $\sqrt{12}$ | C. | $\sqrt{{x}^{2}+1}$ | D. | $\sqrt{4}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com