
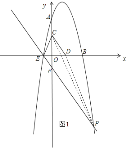
【题目】如图,已知抛物线![]() 与坐标轴分别交于点A(0,8)、B(8,0)和点E,动点C从原点O开始沿OA方向以每秒1个单位长度移动,动点D从点B开始沿BO方向以每秒1个单位长度移动,动点C、D同时出发,当动点D到达原点O时,点C、D停止运动.
与坐标轴分别交于点A(0,8)、B(8,0)和点E,动点C从原点O开始沿OA方向以每秒1个单位长度移动,动点D从点B开始沿BO方向以每秒1个单位长度移动,动点C、D同时出发,当动点D到达原点O时,点C、D停止运动.
(1)直接写出抛物线的解析式: ;
(2)求△CED的面积S与D点运动时间t的函数解析式;当t为何值时,△CED的面积最大?最大面积是多少?
(3)当△CED的面积最大时,在抛物线上是否存在点P(点E除外),使△PCD的面积等于△CED的最大面积?若存在,求出P点的坐标;若不存在,请说明理由.

【答案】(1)![]() ;(2)
;(2)![]() ,当t=5时,S最大=
,当t=5时,S最大=![]() ;(3)存在,P(
;(3)存在,P(![]() ,
,![]() )或P(8,0)或P(
)或P(8,0)或P(![]() ,
,![]() ).
).
【解析】
试题分析:(1)将点A、B代入抛物线即可求出抛物线的解析式;
(2)根据题意得:当D点运动t秒时,BD=t,OC=t,然后由点A(0,8)、B(8,0),可得OA=8,OB=8,从而可得OD=8﹣t,然后令y=0,求出点E的坐标为(﹣2,0),进而可得OE=2,DE=2+8﹣t=10﹣t,然后利用三角形的面积公式即可求△CED的面积S与D点运动时间t的函数解析式为:![]() ,然后转化为顶点式即可求出最值为:S最大=
,然后转化为顶点式即可求出最值为:S最大=![]() ;
;
(3)由(2)知:当t=5时,S最大=![]() ,进而可知:当t=5时,OC=5,OD=3,进而可得CD=
,进而可知:当t=5时,OC=5,OD=3,进而可得CD=![]() ,从而确定C,D的坐标,即可求出直线CD的解析式,然后过E点作EF∥CD,交抛物线与点P,然后求出直线EF的解析式,与抛物线联立方程组解得即可得到其中的一个点P的坐标,然后利用面积法求出点E到CD的距离,过点D作DN⊥CD,垂足为N,且使DN等于点E到CD的距离,然后求出N的坐标,再过点N作NH∥CD,与抛物线交与点P,然后求出直线NH的解析式,与抛物线联立方程组求解即可得到其中的另两个点P的坐标.
,从而确定C,D的坐标,即可求出直线CD的解析式,然后过E点作EF∥CD,交抛物线与点P,然后求出直线EF的解析式,与抛物线联立方程组解得即可得到其中的一个点P的坐标,然后利用面积法求出点E到CD的距离,过点D作DN⊥CD,垂足为N,且使DN等于点E到CD的距离,然后求出N的坐标,再过点N作NH∥CD,与抛物线交与点P,然后求出直线NH的解析式,与抛物线联立方程组求解即可得到其中的另两个点P的坐标.
试题解析:(1)将点A(0,8)、B(8,0)代入抛物线y=﹣![]() x2+bx+c得:
x2+bx+c得: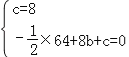 ,解得:b=3,c=8,∴抛物线的解析式为:
,解得:b=3,c=8,∴抛物线的解析式为:![]() ,故答案为:
,故答案为:![]() ;
;
(2)∵点A(0,8)、B(8,0),∴OA=8,OB=8,令y=0,得:![]() ,解得:
,解得:![]() ,
,![]() ,∵点E在x轴的负半轴上,∴点E(﹣2,0),∴OE=2,根据题意得:当D点运动t秒时,BD=t,OC=t,∴OD=8﹣t,∴DE=OE+OD=10﹣t,∴S=
,∵点E在x轴的负半轴上,∴点E(﹣2,0),∴OE=2,根据题意得:当D点运动t秒时,BD=t,OC=t,∴OD=8﹣t,∴DE=OE+OD=10﹣t,∴S=![]() DEOC=
DEOC=![]() (10﹣t)t=
(10﹣t)t=![]() ,即
,即![]() =
=![]() ,∴当t=5时,S最大=
,∴当t=5时,S最大=![]() ;
;
(3)由(2)知:当t=5时,S最大=![]() ,∴当t=5时,OC=5,OD=3,∴C(0,5),D(3,0),由勾股定理得:CD=
,∴当t=5时,OC=5,OD=3,∴C(0,5),D(3,0),由勾股定理得:CD=![]() ,设直线CD的解析式为:
,设直线CD的解析式为:![]() ,将C(0,5),D(3,0),代入上式得:k=
,将C(0,5),D(3,0),代入上式得:k=![]() ,b=5,∴直线CD的解析式为:
,b=5,∴直线CD的解析式为:![]() ,过E点作EF∥CD,交抛物线与点P,如图1,
,过E点作EF∥CD,交抛物线与点P,如图1,
设直线EF的解析式为:![]() ,将E(﹣2,0)代入得:b=
,将E(﹣2,0)代入得:b=![]() ,∴直线EF的解析式为:
,∴直线EF的解析式为:![]() ,将
,将![]() ,与
,与![]() 联立成方程组得:
联立成方程组得: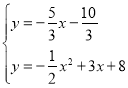 ,解得:
,解得:![]() ,或
,或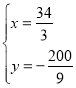 ,∴P(
,∴P(![]() ,
,![]() );
);
过点E作EG⊥CD,垂足为G,∵当t=5时,S△ECD=![]() CDEG=
CDEG=![]() ,∴EG=
,∴EG=![]() ,过点D作DN⊥CD,垂足为N,且使DN=
,过点D作DN⊥CD,垂足为N,且使DN=![]() ,过点N作NM⊥x轴,垂足为M,如图2,
,过点N作NM⊥x轴,垂足为M,如图2,
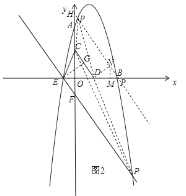
可得△EGD∽△DMN,∴![]() ,∴EGDN=EDDM,即:DM=
,∴EGDN=EDDM,即:DM=![]() =
=![]() ,∴OM=
,∴OM=![]() ,由勾股定理得:MN=
,由勾股定理得:MN=![]() =
=![]() ,∴N(
,∴N(![]() ,
,![]() ),过点N作NH∥CD,与抛物线交与点P,如图2,设直线NH的解析式为:
),过点N作NH∥CD,与抛物线交与点P,如图2,设直线NH的解析式为:![]() ,将N(
,将N(![]() ,
,![]() ),代入上式得:b=
),代入上式得:b=![]() ,∴直线NH的解析式为:
,∴直线NH的解析式为:![]() ,将
,将![]() ,与
,与![]() 联立成方程组得:
联立成方程组得: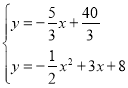 ,解得:
,解得:![]() ,或
,或 ,∴P(8,0)或P(
,∴P(8,0)或P(![]() ,
,![]() ),
),
综上所述:当△CED的面积最大时,在抛物线上存在点P(点E除外),使△PCD的面积等于△CED的最大面积,点P的坐标为:P(![]() ,
,![]() )或P(8,0)或P(
)或P(8,0)或P(![]() ,
,![]() ).
).


科目:初中数学 来源: 题型:
【题目】直线AB、CD相交于点O.
(1)OE、OF分别是∠AOC、∠BOD的平分线.画出这个图形.
(2)射线OE、OF在同一条直线上吗?(直接写出结论)
(3)画∠AOD的平分线OG.OE与OG有什么位置关系?并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线y=x2﹣2mx﹣1(m>0)的顶点M关于坐标原点O的对称点为N,若点N在这条抛物线上,则点M的坐标为( )
A.(﹣1,2)B.(1,﹣2)C.(﹣1,﹣2)D.(1,2)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】用直尺和圆规作一个角等于已知角,如图,能得出∠A′O′B′=∠AOB的依据是( ) 
A.(SAS)
B.(SSS)
C.(ASA)
D.(AAS)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是跷跷板的示意图.支柱OC与地面垂直,点O是横板AB的中点,AB可以绕着点O上下转动,当A端落地时,∠OAC=20°,跷跷板上下可转动的最大角度(即∠A′OA)是( ) 
A.80°
B.60°
C.40°
D.20°
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com