
【题目】△ABC中,BC=8,以AC为边向外作等边△ACD.
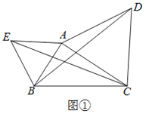
(1)如图①,△ABE是等边三角形,若AC=6,∠ACB=30°,求CE的长;
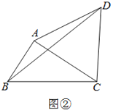
(2)如图②,若∠ABC=60°,AB=4,求BD的长.
【答案】(1)10;(2)![]()
【解析】
(1)根据等边三角形的性质及等式的性质求得![]() ,然后利用边角边定理证明
,然后利用边角边定理证明![]() ,从而求得
,从而求得![]() ,然后判定
,然后判定![]() 为直角三角形,利用勾股定理求BD的长,使问题得解;
为直角三角形,利用勾股定理求BD的长,使问题得解;
(2)取![]() 的中点
的中点![]() ,连接
,连接![]() ,求得
,求得![]() 是等边三角形,
是等边三角形,![]() 是等腰三角形,从而求得
是等腰三角形,从而求得![]() ,∠BAC=90° ,然后利用勾股定理求解.
,∠BAC=90° ,然后利用勾股定理求解.
(1)∵![]() 和
和![]() 都是等边三角形.
都是等边三角形.
∴![]() ,
,![]()
![]()
∴![]()
∴![]()
∴![]() ,
,
∴![]()
∵![]() ,
,![]()
∴![]() ,
,![]() 为直角三角形.
为直角三角形.
∴![]()
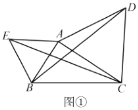
(2)取![]() 的中点
的中点![]() ,连接
,连接![]() ,
,
∵BC=8,∴BE=CE=AB=4
又∵∠ABC=60°
∴![]() 是等边三角形,
是等边三角形,![]() 是等腰三角形,
是等腰三角形,
∴∠AEB=2∠ECA=60°,即∠ECA=30°
由△ADC为等边三角形,可知∠ACD=60°
∴![]() ,∠BAC=90°
,∠BAC=90°
∴在Rt△ABC中,![]()
∴在Rt△BCD中,![]()



科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD的面积为16cm2,△AEF为等腰直角三角形,∠E=90°,AE和BC交于点G,AF和CD交于点H,则△CGH的周长( )

A. 4cmB. 6cmC. 8cmD. 10cm
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,点O是AC边上的一个动点,过点O作直线MN∥BC,设MN交∠BCA的平分线于点E,交∠BCA的外角平分线于点F.
(1)判断OE与OF的大小关系?并说明理由?
(2)当点O运动何处时,四边形AECF是矩形?并说出你的理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个不透明的袋中装有5个黄球、13个黑球和22个红球,这些球除颜色外其他都相同.
(1)求从袋中摸出一个球是黄球的概率;
(2)求从袋中摸出一个球不是红球的概率;
(3)现在从袋中取出若干个黑球,并放入相同数量的黄球,搅拌均匀后,若从袋中摸出一个球是黄球的概率为![]() ,则取出了多少个黑球?
,则取出了多少个黑球?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲乙两位同学利用灯光下的影子来测量一路灯A的高度,如图,当甲走到点C处时,乙测得甲直立身高CD与其影子长CE正好相等,接着甲沿BC方向继续向前走,走到点E处时,甲直立身高EF的影子恰好是线段EG,并测得EG=2.5m.已知甲直立时的身高为1.75m,求路灯的高AB的长.(结果精确到0.1m)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】四边形ABCD中,对角线AC、BD相交于点O,下列条件不能判定这个四边形是平行四边形的是

A.AB∥DC,AD∥BC B.AB=DC,AD=BC
C.AO=CO,BO=DO D.AB∥DC,AD=BC
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平行四边形ABCD中,∠BAD、∠ABC的平分线AF、BG分别与线段CD交于点F、G,
AF与BG交于点E.

(1)求证:AF⊥BG,DF=CG;
(2)若AB=10,AD=6,AF=8,求FG和BG的长度.
查看答案和解析>>
科目:初中数学 来源: 题型:
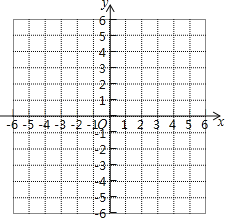
【题目】如图是一个平面直角坐标系.
(1)请在图中描出以下6个点:A(0,2)、B(4,2)、C(3,4)A′(-4,-4)、B'(0,-4)、C′(-1,-2)
(2)分别顺次连接A、B、C和A′、B'、C',得到三角形ABC和三角形A′B′C′;
(3)观察所画的图形,判断三角形A′B′C′能否由三角形ABC平移得到,如果能,请说出三角形A′B′C′是由三角形ABC怎样平移得到的;如果不能,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】材料阅读:材料1:符号“ ”称为二阶行列式,规定它的运算法则为
”称为二阶行列式,规定它的运算法则为 .如
.如![]() .
.
材料2:我们已经学习过求解一元一次方程、二元一次方程组、分式方程等方程的解法,虽然各类方程的解法不尽相同,但是蕴含了相同的基本数学思想——转化,把未知转化为已知.用“转化”的数学思想,还可以解一些新的方程.例如,求解部分一元二次方程![]() 时,我们可以利用因式分解把它转化为一元一次方程来求解.如解方程:
时,我们可以利用因式分解把它转化为一元一次方程来求解.如解方程:![]() .∵
.∵![]() ∴
∴![]() .故
.故![]() 或
或![]() .因此原方程的解是
.因此原方程的解是![]() ,
,![]() .
.
根据材料回答以下问题:
(1)二阶行列式![]() ___________;二阶行列式
___________;二阶行列式![]() 中
中![]() 的值为__________.
的值为__________.
(2)求解![]() 中
中![]() 的值.
的值.
(3)结合材料,若![]() ,
,![]() ,且
,且![]() ,求
,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com