练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】甲乙两位同学利用灯光下的影子来测量一路灯A的高度，如图，当甲走到点C处时，乙测得甲直立身高CD与其影子长CE正好相等，接着甲沿BC方向继续向前走，走到点E处时，甲直立身高EF的影子恰好是线段EG，并测得EG=2.5m.已知甲直立时的身高为1.75m，求路灯的高AB的长.（结果精确到0.1m）

    【答案】路灯高AB约为5.8米.

    【解析】试题分析：根据EF⊥BC，CD⊥BC，AB⊥BC，得到AB∥CD∥EF，从而得到△ABN∽△ACD，利用相似三角形对应边的比相等列出比例式求解即可．

    解：如图，设AB= x，

    由题意知AB⊥BG，CD⊥BG，FE⊥BG，CD=CE，

    ∴AB∥CD∥EF，∴BE=AB=x，

    ∴△ABG∽△FEC

    ∴，即，

    ∴m

    答：路灯高AB约为5.8米.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】如图，四幅图象分别表示变量之间的关系，请按图象的顺序，将下面的四种情境与之对应排序．正确的顺序是（　　）

    ①篮球运动员投篮时，投出去的篮球的高度与时间的关系；

    ②去超市购买同一单价的水果，所付费用与水果数量的关系；

    ③李老师使用的是一种含月租的手机计费方式，则他每月所付话费与通话时间的关系；

    ④周末，小明从家到图书馆，看了一段时间书后，按原速度原路返回，小明离家的距离与时间的关系

    A. B. C. D.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，二次函数y=ax2﹣4x+c的图象经过坐标原点，与x轴交于点A（﹣4，0）．

    （1）求二次函数的解析式；

    （2）在抛物线上存在点P，满足S△AOP=8，请直接写出点P的坐标．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】盒中有若干枚黑棋和白棋，这些棋除颜色外无其他差别，现让学生进行摸棋试验：每次摸出一枚棋，记录颜色后放回摇匀，重复进行这样的试验得到以下数据：

    摸棋的次数n

    100

    200

    300

    500

    800

    1000

    摸到黑棋的次数m

    24

    51

    76

    b

    201

    250

    摸到黑棋的频率（精确到0.001）

    0.240

    a

    0.253

    0.248

    0.251

    0.250

    （1）填空：a=　 　，b=　 　；

    （2）在图中，画出摸到黑棋的折线统计图；

    （3）随机摸一次，估计摸到黑棋的概率．（精确到0.01）

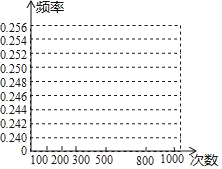
    查看答案和解析>>

    科目：初中数学 来源： 题型：

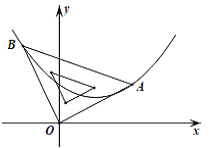
    【题目】如图，二次函数的图象的顶点坐标为（1， ），现将等腰直角三角板直角顶点放在原点O，一个锐角顶点A在此二次函数的图象上，而另一个锐角顶点B在第二象限，且点A的坐标为（2，1）.

    （1）求该二次函数的表达式；

    （2）判断点B是否在此二次函数的图象上，并说明理由.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】△ABC中，BC＝8，以AC为边向外作等边△ACD．

    （1）如图①，△ABE是等边三角形，若AC＝6，∠ACB＝30°，求CE的长；

    （2）如图②，若∠ABC＝60°，AB＝4，求BD的长．

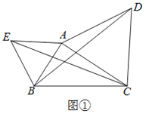
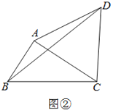
    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，已知函数y1＝x＋5的图象与x轴交于点A，一次函数y2＝－2x＋b的图象分别与x轴、y轴交于点B，C，且与y1＝x＋5的图象交于点D（m，4）．

    （1）求m，b的值；

    （2）若y1＞y2，则x的取值范围是　 ；

    （3）求四边形AOCD的面积．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】用适当的方法解下列方程．

    (1).x2－2x＝2x＋1；

    (2).(x＋3)2＝(1－2x)2.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】甲、乙两人进行羽毛球比赛，羽毛球飞行的路线为抛物线的一部分，如图，甲在O点正上方1m的P处发出一球，羽毛球飞行的高度y（m）与水平距离x（m）之间满足函数表达式y=a（x﹣4）2+h，已知点O与球网的水平距离为5m，球网的高度为1.55m．

    （1）当a=﹣时，①求h的值；②通过计算判断此球能否过网．

    （2）若甲发球过网后，羽毛球飞行到与点O的水平距离为7m，离地面的高度为m的Q处时，乙扣球成功，求a的值．

    查看答案和解析>>

    同步练习册答案