
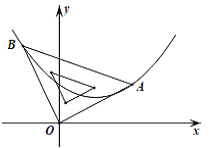
【题目】如图,二次函数的图象的顶点坐标为(1, ![]() ),现将等腰直角三角板直角顶点放在原点O,一个锐角顶点A在此二次函数的图象上,而另一个锐角顶点B在第二象限,且点A的坐标为(2,1).
),现将等腰直角三角板直角顶点放在原点O,一个锐角顶点A在此二次函数的图象上,而另一个锐角顶点B在第二象限,且点A的坐标为(2,1).
(1)求该二次函数的表达式;
(2)判断点B是否在此二次函数的图象上,并说明理由.
科目:初中数学 来源: 题型:
【题目】小武新家装修,在装修客厅时,购进彩色地砖和单色地砖共100块,共花费5600元.已知彩色地砖的单价是80元/块,单色地砖的单价是40元/块.
(1)两种型号的地砖各采购了多少块?
(2)如果厨房也要铺设这两种型号的地砖共60块,且采购地砖的费用不超过3200元,那么彩色地砖最多能采购多少块?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,如图,抛物线y=x2+bx+c与x轴交于点A和点B(4,0),与y轴交于点C(0,4).
(1)求抛物线的解析式;
(2)若点M是抛物线在x轴下方的动点,过点M作MN∥y轴交直线BC于点N求线段MN的最大值;(3)在(2)的条件下,当MN取得最大值时,在抛物线的对称轴l上是否存在点P使△PBN是等腰三角形?若存在,请直接写出所有点P的坐标;若不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】两幢大楼的部分截面及相关数据如图,小明在甲楼A处透过窗户E发现乙楼F处出现火灾,此时A,E,F在同一直线上.跑到一楼时,消防员正在进行喷水灭火,水流路线呈抛物线,在1.2m高的D处喷出,水流正好经过E,F. 若点B和点E、点C和F的离地高度分别相同,现消防员将水流抛物线向上平移0.4m,再向左后退了____m,恰好把水喷到F处进行灭火.

查看答案和解析>>
科目:初中数学 来源: 题型:
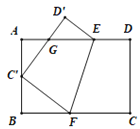
【题目】如图,将矩形ABCD沿EF折叠,使顶点C恰好落在AB边的C'处,点D落在点D'处,C'D'交线段AE于点G.
(1)求证:△BC'F∽△AGC';
(2)若C'是AB的中点,AB=6,BC=9,求AG的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲乙两位同学利用灯光下的影子来测量一路灯A的高度,如图,当甲走到点C处时,乙测得甲直立身高CD与其影子长CE正好相等,接着甲沿BC方向继续向前走,走到点E处时,甲直立身高EF的影子恰好是线段EG,并测得EG=2.5m.已知甲直立时的身高为1.75m,求路灯的高AB的长.(结果精确到0.1m)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,物理实验室有一单摆在左右摆动,摆动过程中选取了两个瞬时状态,从C处测得E、F两点的俯角分别为∠ACE=60°,∠BCF=45°,这时点F相对于点E升高了4cm.求该摆绳CD的长度.(精确到0.1cm,参考数据: ![]() ≈1.41,
≈1.41, ![]() ≈1.73)
≈1.73)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一块三角形模具的阴影部分已破损.回答下列问题:
(1)只要从模具片中度量出哪些边、角,就可以到店铺加工一块与原来的模具△ABC的形状和大小完全相同的△A′B′C′模具?请简要说明理由.
(2)按尺规作图的要求,在框内正确作出△A′B′C′图形,保留作图痕迹,不写作法和证明.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某天早上,住在同一小区的小雨、小静两人从小区出发,沿相同的路线步行到学校上学.小雨出发5分钟后,小静才出发,同时小雨发现自己没带手表,于是决定按原速回家拿手表小雨拿到手表后,担心会迟到,于是速度提高了20%,结果比小静早2分钟到校.小雨取手表的时间忽略不计,在整个过程中,小静始终保持匀速运动,小雨提速前后也分别保持匀速运动,如图所示是小雨、小静之间的距离![]() (米)与小雨离开小区的时间
(米)与小雨离开小区的时间![]() (分钟)之间的函数图像,则小区到学校的距离是_______米.
(分钟)之间的函数图像,则小区到学校的距离是_______米.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com