
【题目】如图,如图,抛物线y=x2+bx+c与x轴交于点A和点B(4,0),与y轴交于点C(0,4).
(1)求抛物线的解析式;
(2)若点M是抛物线在x轴下方的动点,过点M作MN∥y轴交直线BC于点N求线段MN的最大值;(3)在(2)的条件下,当MN取得最大值时,在抛物线的对称轴l上是否存在点P使△PBN是等腰三角形?若存在,请直接写出所有点P的坐标;若不存在,请说明理由.

【答案】(1)y=x2-5x+4;(2)点p的坐标为(![]() ,
,![]() )、(
)、(![]() ,
,![]() ),(
),(![]() -
-![]() )、(
)、(![]() ,2+
,2+![]() ),或(
),或(![]() ,2-
,2-![]() ).
).
【解析】试题分析:
(1)把点B、C的坐标代入![]() 列出方程组,解方程组求得
列出方程组,解方程组求得![]() 的值即可得到二次函数的解析式;
的值即可得到二次函数的解析式;
(2)由点B、C的坐标可求出直线BC的解析式,设点M的横坐标为m,由此可用含m的代数式表示出点M、N的纵坐标,从而可用含m的式子表达出MN的长度,由点M在![]() 轴下方可求得m的取值范围为:
轴下方可求得m的取值范围为: ![]() ,由此即可求出线段MN的最大值;
,由此即可求出线段MN的最大值;
(3)由题意结合(2)可得点N的坐标,由点P在抛物线对称轴上,可设其坐标为(2.5,n),结合点B和点N的坐标即可表达出PB、PN、BN的长度,再分PB=PN、PB=BN、PN=BN三种情况讨论计算即可求得符合题意的点P的坐标.
试题解析:
(1)将点B(4,0)、C(0,4)代入抛物线y=x2+bx+c中,
得![]() ,得
,得![]() ,
,
∴抛物线的解析式为y=x2-5x+4.
(2)由题意可设点M的坐标为(m,m2-5m+4),设直线BC的解析式为y=kx+4,
把点(4,0)代入y=kx+4,中,
得:0=4k+4,解得:k=-1,
∴直线BC的解析式为y=-x+4.
∵MN∥y轴,
∴点N的坐标为(m,-m+4),
∴MN==-m+4-(m2-5m+4)=-(m-2)2+4.
∵抛物线的解析式为:y=x2-5x+4=(x-2.5)2,
∴抛物线的对称轴为x=2.5,
∴由点B的坐标为(4,0)可得点A的坐标为(1,0),
又∵点M在x轴下方,
∴1<m<4.
∴当m=2时,MN最大=4.
(3)由(2)可得:当m=2时,点N的坐标为(2,2),
∵点P在抛物线的对称轴上,
∴可设点P坐标为(2.5,n),
∴PB=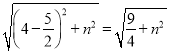 ,PN=
,PN= =
=![]() ,
,
BN=![]() =2
=2![]() ,
,
若![]() 为等腰三角形,则存在以下三种情况:
为等腰三角形,则存在以下三种情况:
①当![]() 时,即
时,即![]()
![]()
解得: ![]() ,此时点
,此时点![]() 的坐标为(
的坐标为(![]() ,
, ![]() );
);
②当![]() 时,即
时,即![]() =2
=2![]() ,解得:
,解得: ![]() ,
,
此时点![]() 的坐标为(
的坐标为(![]() ,
, ![]() )或(
)或(![]() ,
, ![]() );
);
③当![]() 时,即
时,即![]() =2
=2![]() ,解得:
,解得: ![]() ,
,
此时点![]() 的坐标为(
的坐标为(![]() ,2+
,2+![]() )或(
)或(![]() ,2
,2![]() ).
).
综上可知:在抛物线的对称轴![]() 上存在点
上存在点![]() ,使
,使![]() 是等腰三角形,点P的坐标为(
是等腰三角形,点P的坐标为(![]() ,
,![]() )、(
)、(![]() ,
,![]() ),(
),(![]() -
-![]() )、(
)、(![]() ,2+
,2+![]() ),或(
),或(![]() ,2-
,2-![]() ).
).


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图,直线AB∥CD,∠FGH=90°,∠GHM= 40°,∠HMN=30°,并且∠EFA的两倍比∠CNP大10°,则∠PND的大小是( )

A. 100°B. 120°C. 130°D. 150°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,半圆O的直径AB=20,将半圆O绕点B顺针旋转45°得到半圆O′,与AB交于点P.
(1)求AP的长;
(2)求图中阴影部分的面积(结果保留π).


查看答案和解析>>
科目:初中数学 来源: 题型:
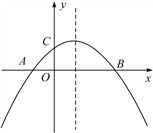
【题目】如图,二次函数y=ax2+bx+c(a≠0)的图象与x轴交于A,B两点,与y轴交于点C,且OA=OC.则下列结论:①abc<0;②![]() >0;③ac-b+1=0;④OA·OB=-
>0;③ac-b+1=0;④OA·OB=-![]() .其中结论正确的是____________
.其中结论正确的是____________
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(本题10分)光伏发电惠民生,据衢州晚报载,某家庭投资4万元资金建造屋顶光伏发电站,遇到晴天平均每天可发电30度,其他天气平均每天可发电5度.已知某月(按30天计)共发电550度.
(1)求这个月晴天的天数;
(2)已知该家庭每月平均用电量为150度,若按每月发电550度计,至少需要几年才能收回成本.(不计其他费用,结果取整数).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,二次函数y=ax2﹣4x+c的图象经过坐标原点,与x轴交于点A(﹣4,0).

(1)求二次函数的解析式;
(2)在抛物线上存在点P,满足S△AOP=8,请直接写出点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠ACB=90°,∠B=30°,将△ABC绕点C按顺时针方向旋转n度后,得到△DEC,点D刚好落在AB边上.

(1)求n的值;
(2)若F是DE的中点,判断四边形ACFD的形状,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
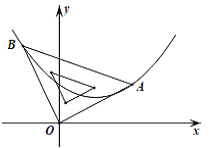
【题目】如图,二次函数的图象的顶点坐标为(1, ![]() ),现将等腰直角三角板直角顶点放在原点O,一个锐角顶点A在此二次函数的图象上,而另一个锐角顶点B在第二象限,且点A的坐标为(2,1).
),现将等腰直角三角板直角顶点放在原点O,一个锐角顶点A在此二次函数的图象上,而另一个锐角顶点B在第二象限,且点A的坐标为(2,1).
(1)求该二次函数的表达式;
(2)判断点B是否在此二次函数的图象上,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下列材料:
我们知道方程2x+3y=12有无数组解,但在实际生活中我们往往只需要求出其正整数解.例:由2x+3y=12,得y=![]() =4-
=4-![]() x,(x、y为正整数)
x,(x、y为正整数)
∴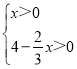 则有0<x<6
则有0<x<6
又y=4-![]() x为正整数,则
x为正整数,则![]() x为正整数.
x为正整数.
从而x=3,代入y=4-![]() ×3=2
×3=2
∴2x+3y=12的正整数解为![]() .
.
利用以上方法解决下列问题:
七年级某班为了奖励学习进步的学生,购买了单价为3元的笔记本与单价为5元的钢笔两种奖品,共花费35元,问有几种购买方案?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com