
【题目】如图,直线AB∥CD,∠FGH=90°,∠GHM= 40°,∠HMN=30°,并且∠EFA的两倍比∠CNP大10°,则∠PND的大小是( )

A. 100°B. 120°C. 130°D. 150°
【答案】C
【解析】
作辅助线:延长PM、EG交于点K;EG的延长线交CD于点O,PM延长线交AB于点L,利用平行线性质进行求解.
延长PM、EG交于点K;EG的延长线交CD于点O,PM延长线交AB于点L,如图,
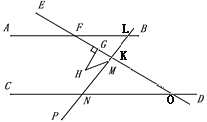
∵∠HMN=30゜,
∴∠HMK=150゜,
在四边形GHMK中,∠HGK=90゜,∠GHM=40゜,∠HMK=150゜,
∴∠GKM=360゜-∠HGK-∠GHM-∠HMK=360゜-90゜-40゜-150゜=80゜,
∴∠FKL=100゜,
∴∠NKO=100゜,
设∠EFA =x,则∠PNC =2x-10゜,
∴∠KNO=2x-10゜,
∵AB∥CD,
∴∠KON=∠EFA=x,
∵∠KNO+∠NKO+∠KON=180゜,
∴2x-10゜+x+100゜=180゜,解得,x=30゜,
∴∠PNC=2×30゜-10゜=50゜,
∴∠PND=180゜-50゜=130゜.
故选C.


科目:初中数学 来源: 题型:
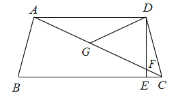
【题目】如图,在四边形 ABCD 中,AD∥BC,DE⊥BC,垂足为点 E,连接 AC 交DE 于点 F,点 G 为 AF 的中点,∠ACD=2∠ACB,若 DC=5,则 AF 的长为___________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校九年级(1)班所有学生参加2010年初中毕业生升学体育测试,根据测试评分标准,将他们的成绩进行统计后分为A、B、C、D四等,并绘制成如图所示的条形统计图和扇形统计图(未完成),请结合图中所给信息解答下列问题:

(1)九年级(1)班参加体育测试的学生有 人;
(2)将条形统计图补充完整;
(3)在扇形统计图中,等级B部分所占的百分比是 ,等级C对应的圆心角的度数为 ;
(4)若该校九年级学生共有850人参加体育测试,估计达到A级和B级的学生共有 人.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某饮料厂开发了A、B两种新型饮料,主要原料均为甲和乙,每瓶饮料中甲、乙的含量如下表所示.现用甲原料和乙原料各2800克进行试生产,计划生产A、B两种饮料共100瓶.设生产A种饮料x瓶,解析下列问题:
原料名称 饮料名称 | 甲 | 乙 |
A | 20克 | 40克 |
B | 30克 | 20克 |
(1)有几种符合题意的生产方案写出解析过程;
(2)如果A种饮料每瓶的成本为2.60元,B种饮料每瓶的成本为2.80元,这两种饮料成本总额为y元,请写出y与x之间的关系式,并说明x取何值会使成本总额最低?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了测量一个圆铁环的半径,某同学用了如下方法,将铁环平放在水平桌面上,用有一个角为30°的直角三角板和刻度尺按如图所示的方法得到相关数据,进而求出铁环半径,若测得PA=5cm,则铁环的半径是_____cm.

查看答案和解析>>
科目:初中数学 来源: 题型:
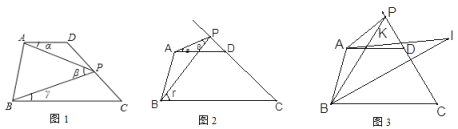
【题目】如图,已知四边形ABCD,AD∥BC.点P在直线CD上运动(点P和点C,D不重合,点P,A,B不在同一条直线上),若记∠DAP,∠APB,∠PBC分别为∠α,∠β,∠γ.
(1)如图1,当点P在线段CD上运动时,写出∠α,∠β,∠γ之间的关系并说出理由;
(2)如图2,如果点P在线段CD的延长线上运动,探究∠α,∠β,∠γ之间的关系,并说明理由.
(3)如图3,BI平分∠PBC,AI交BI于点I,交BP于点K,且∠PAI:∠DAI=5:1,∠APB=20°,∠I=30°,求∠PAI的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在长方形OABC中,O为平面直角坐标系的原点,点A坐标为C(a,0),点C的坐标为(0,b),且a,b满足(a﹣4)2+|b﹣6|=0,点B在第一象限内,点P从原点出发,以每秒2个单位长度的速度沿着O→C→B→A→O的路线移动.
(1)a= ,b= ,点B的坐标为 .
(2)当点P移动4秒时,请说明点P的位置,并求出点P的坐标;
(3)在移动过程中,当点P到x轴的距离为5个单位长度时,求点P移动的时间.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小武新家装修,在装修客厅时,购进彩色地砖和单色地砖共100块,共花费5600元.已知彩色地砖的单价是80元/块,单色地砖的单价是40元/块.
(1)两种型号的地砖各采购了多少块?
(2)如果厨房也要铺设这两种型号的地砖共60块,且采购地砖的费用不超过3200元,那么彩色地砖最多能采购多少块?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,如图,抛物线y=x2+bx+c与x轴交于点A和点B(4,0),与y轴交于点C(0,4).
(1)求抛物线的解析式;
(2)若点M是抛物线在x轴下方的动点,过点M作MN∥y轴交直线BC于点N求线段MN的最大值;(3)在(2)的条件下,当MN取得最大值时,在抛物线的对称轴l上是否存在点P使△PBN是等腰三角形?若存在,请直接写出所有点P的坐标;若不存在,请说明理由.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com