
如图,抛物线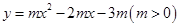 与
与 轴交于
轴交于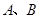 两点,与
两点,与 轴交于
轴交于 点.
点.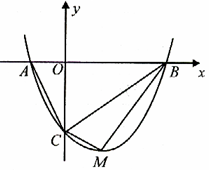
(1)请求出抛物线顶点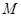 的坐标(用含
的坐标(用含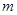 的代数式表示),
的代数式表示),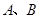 两点的坐标;
两点的坐标;
(2)经探究可知, 与
与 的面积比不变,试求出这个比值;
的面积比不变,试求出这个比值;
(3)是否存在使 为直角三角形的抛物线?若存在,请求出;如果不存在,请说明理由.
为直角三角形的抛物线?若存在,请求出;如果不存在,请说明理由.
解析试题分析:(1)将抛物线的解析式化为顶点坐标式,即可得到顶点M的坐标;抛物线的解析式中,令y=0,可求得A、B的坐标.
(2)易求得C点坐标,即可得到OC的长,以AB为底,OC为高,即可求出△ABC的面积;△BCM的面积无法直接求得,可用割补法求解,过M作MD⊥x轴于D,根据B、C、M四点坐标,可分别求出梯形OCMD、△BDM的面积,它们的面积和减去△BOC的面积即为△BCM的面积,进而可得到△ABC、△BCM的面积比.
(3)首先根据B、C、M的坐标,求出BC2、BM2、CM2的值,由于△BCM中,B、C、M都有可能是直角顶点,所以要分三种情况讨论:①∠BCM=90°,②∠BMC=90°,③∠MBC=90°,在上述三种不同的直角三角形中,利用勾股定理可求得m的值,进而可确定抛物线的解析式.
(1)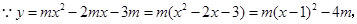
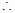 抛物线顶点
抛物线顶点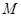 的坐标为(1,
的坐标为(1, m)
m)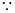 抛物线
抛物线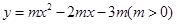 与
与 轴交于
轴交于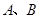 两点,
两点,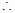 当
当 时,
时,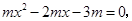
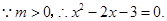
解得
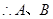 两点的坐标为(
两点的坐标为( )、(
)、(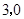 );
);
(2)当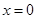 时,
时, ,
,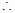 点
点 的坐标为
的坐标为 .
.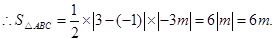 5分
5分
过点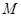 作
作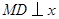 轴于点
轴于点 ,则
,则
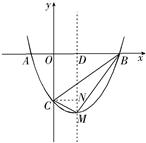
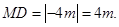
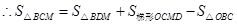
=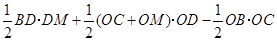
=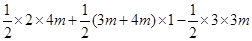
=3m
(3)存在使 为直角三角形的抛物线.
为直角三角形的抛物线.
过点 作
作 于点
于点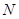 ,则
,则 为
为 ,
,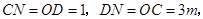
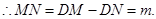
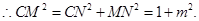
在 中,
中,
在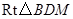 中,
中,
①如果 是
是 ,且
,且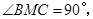 那么
那么
即
解得 ,
,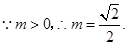
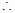 存在抛物线
存在抛物线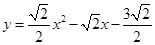 使得
使得 是
是 ;
;
②如果 是
是 ,且
,且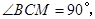 那么
那么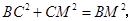
即
解得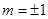 ,
,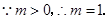
 存在抛物线
存在抛物线 ,使得
,使得 是
是 ;
;
③如果 是
是 ,且
,且 ,那么
,那么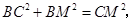
即
整理得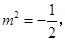 此方程无解.
此方程无解. 以
以


科目:初中数学 来源: 题型:
如图,抛物线与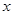 轴交于
轴交于![]() (
(![]() ,0)、
,0)、![]() (
(![]() ,0)两点,且
,0)两点,且![]() ,与
,与![]() 轴交于点
轴交于点![]() ,其中
,其中![]() 是方程
是方程![]() 的两个根。(14分)
的两个根。(14分)
(1)求抛物线的解析式;
 (2)点
(2)点![]() 是线段
是线段![]() 上的一个动点,过点
上的一个动点,过点![]() 作
作![]() ∥
∥![]() ,交
,交![]() 于点
于点![]() ,连接
,连接![]() ,当
,当![]() 的面积最大时,求点
的面积最大时,求点![]() 的坐标;
的坐标;
(3)点![]() 在(1)中抛物线上,
在(1)中抛物线上,
点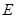 为抛物线上一动点,在
为抛物线上一动点,在![]() 轴上是
轴上是
否存在点 ,使以
,使以![]() 为顶
为顶
点的四边形是平行四边形,如果存在,
求出所有满足条件的点![]() 的坐标,
的坐标,
若不存在,请说明理由。
查看答案和解析>>
科目:初中数学 来源: 题型:
如图,抛物线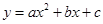 与
与![]() 轴交于
轴交于![]() 两点,与
两点,与![]() 轴相交于点
轴相交于点![]() .连结AC、BC,B、C两点的坐标分别为B(1,0)、
.连结AC、BC,B、C两点的坐标分别为B(1,0)、![]() ,且当x=-10和x=8时函数的值
,且当x=-10和x=8时函数的值![]() 相等.
相等.
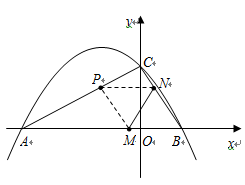
1.求a、b、c的值;
2.若点![]() 同时从
同时从![]() 点出发,均以每秒1个单位长度的速度分别沿
点出发,均以每秒1个单位长度的速度分别沿![]() 边运动,其中一个点到达终点时,另一点也随之停止运动.连结
边运动,其中一个点到达终点时,另一点也随之停止运动.连结![]() ,将
,将![]() 沿
沿![]() 翻折,当运动时间为几秒时,
翻折,当运动时间为几秒时,![]() 点恰好落在
点恰好落在![]() 边上的
边上的![]() 处?并求点
处?并求点![]() 的坐标及四边形
的坐标及四边形![]() 的面积;
的面积;
3.上下平移该抛物线得到新的抛物线,设新抛物线的顶点为D,对称轴与x轴的交点为E,若△ODE与△OBC相似,求新抛物线的解析式。
查看答案和解析>>
科目:初中数学 来源: 题型:
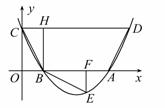
如图,抛物线![]() 与
与![]() 轴交于A、B两点,与
轴交于A、B两点,与![]() 轴交于C点,四边形OBHC为矩形,CH的延长
轴交于C点,四边形OBHC为矩形,CH的延长![]() 线交抛物线于点D(5,2),连结BC、AD.
线交抛物线于点D(5,2),连结BC、AD.
(1)求C点的坐标及抛物线的解析式;
(2)将△BCH绕点B按顺时针旋转90º后再沿![]() 轴对折得到△BEF(点C与点E对应),判断点E是否落在抛物线上,并说明理由;
轴对折得到△BEF(点C与点E对应),判断点E是否落在抛物线上,并说明理由;
(3)设过点E的直线交AB边于点P,交CD边于点Q. 问是否存在点P,使直线PQ分梯形ABCD的面积为1∶3两部分?若存在,求出P点坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源:2012届仙师中学九年级第一次月考试考试数学卷 题型:选择题
如图,抛物线与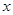 轴交于
轴交于 (
( ,0)、
,0)、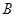 (
( ,0)两点,且
,0)两点,且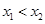 ,与
,与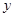 轴交于点
轴交于点 ,其中
,其中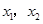 是方程
是方程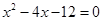 的两个根。(14分)
的两个根。(14分)
(1)求抛物线的解析式;
 (2)点
(2)点 是线段
是线段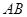 上的一个动点,过点
上的一个动点,过点 作
作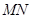 ∥
∥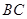 ,交
,交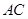 于点
于点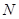 ,连接
,连接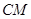 ,当
,当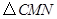 的面积最大时,求点
的面积最大时,求点 的坐标;
的坐标;
(3)点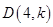 在(1)中抛物线上,
在(1)中抛物线上,
点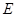 为抛物线上一动点,在
为抛物线上一动点,在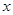 轴上是
轴上是
否存在点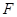 ,使以
,使以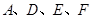 为顶
为顶
点的四边形是平行四边形,如果存在,
求出所有满足条件的点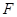 的坐标,
的坐标,
若不存在,请说明理由。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com