
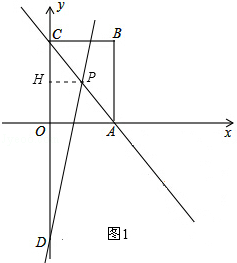
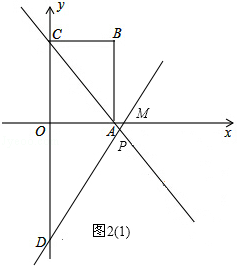
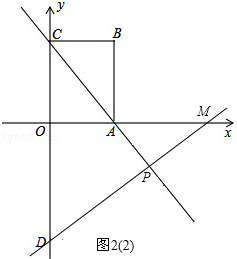
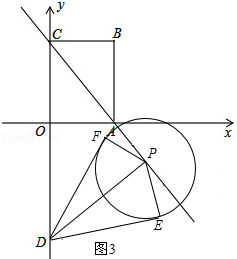
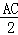 ������D����ԲP�����������붯ԲP�ֱ������ڵ�E��F����̽���ڶ�ԲP���Ƿ���������С���ı���DEPF�������ڣ��������С���S��ֵ���������ڣ���˵�����ɣ�
������D����ԲP�����������붯ԲP�ֱ������ڵ�E��F����̽���ڶ�ԲP���Ƿ���������С���ı���DEPF�������ڣ��������С���S��ֵ���������ڣ���˵�����ɣ�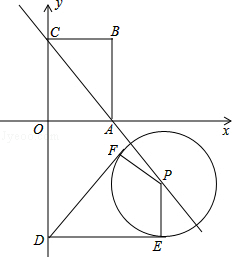
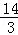 x��5
x��5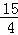 ��0����
��0����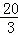 ��0��
��0��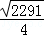
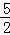 DE���ɡ�DEP=90���DE2=DP2��PE2=DP2��
DE���ɡ�DEP=90���DE2=DP2��PE2=DP2��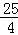 �����ݡ��㵽ֱ��֮�䣬���߶���̡��ɵã���DP��ACʱ��DP��̣���ʱDEҲ��̣���Ӧ���ı���DEPF�������С�����������������ƣ��������DP��ACʱDP��ֵ���Ϳ�����ı���DEPF�������Сֵ��
�����ݡ��㵽ֱ��֮�䣬���߶���̡��ɵã���DP��ACʱ��DP��̣���ʱDEҲ��̣���Ӧ���ı���DEPF�������С�����������������ƣ��������DP��ACʱDP��ֵ���Ϳ�����ı���DEPF�������Сֵ��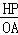 =
=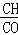 =
=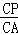 ��
�� CA��
CA�� OA��CH=
OA��CH= CO��
CO��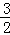 ��CH=2��
��CH=2��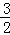 ��2����
��2����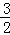 ��2����ֱ��DP�ϣ�
��2����ֱ��DP�ϣ�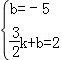
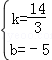
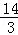 x��5��
x��5��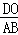 =
=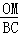 ��
��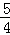 =
=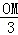 ��
��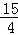 ��
��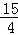 ��0��
��0��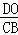 =
=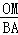 ��
��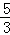 =
=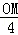 ��
��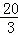 ��
��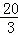 ��0����
��0����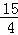 ��0����
��0����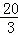 ��0����
��0����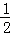 AC=
AC=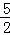 ��
��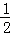 PE•DE=PE•DE=
PE•DE=PE•DE=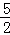 DE��
DE��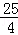 ��
��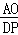 =
=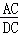 ��
��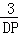 =
=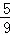 ��
��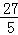 ��
��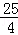 =��
=��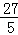 ��2��
��2��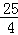 =
=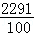 ��
��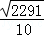 ��
��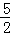 DE=
DE=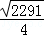 ��
��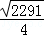 ��
��


 ��Կ���Ծ�ϵ�д�
��Կ���Ծ�ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ������ ���ͣ������
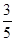 ��OA=10cm����AB��Ϊ cm��
��OA=10cm����AB��Ϊ cm��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ������ ���ͣ���ѡ��
| A��2r=R | B��
| C��3r=R | D��4r=R |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ������ ���ͣ������
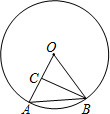
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ������ ���ͣ������
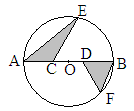
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ������ ���ͣ���ѡ��
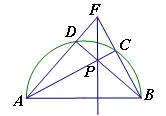
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ������ ���ͣ���ѡ��
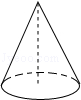
| A��3�� | B��3 | C��6�� | D��6 |
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com