
【题目】如图,点O是等边△ABC内一点,∠AOB=110°,∠BOC=a.将△BOC绕点C按顺时针方向旋转60°得△ADC,连接OD.
(1)求证:△COD是等边三角形;
(2)当a=150°时,试判断△AOD的形状,并说明理由;
(3)探究:当a为多少度时,△AOD是等腰三角形?

【答案】(1)证明见解析;(2)当α=150°时,△AOD是直角三角形,理由见解析;(3)当α的度数为125°或110°或140°时,△AOD是等腰三角形.
【解析】(1)根据旋转的性质可得出OC=OD,结合题意即可证得结论;
(2)结合(1)的结论可作出判断;
(3)找到变化中的不变量,然后利用旋转及全等的性质即可做出解答.
(1)证明:∵将△BOC绕点C按顺时针方向旋转60°得△ADC
∴CO=CD,∠OCD=60°
∴△COD是等边三角形.
(2)解:当![]() =150°时,△AOD是直角三角形
=150°时,△AOD是直角三角形
理由是:∵△BOC≌△ADC
∴∠ADC=∠BOC=150°
又∵△COD是等边三角形
∴∠ODC=60°[来
∴∠ADO=∠ADC -∠ODC=90°,即△AOD是直角三角形.
(3)解:①要使AO=AD,需∠AOD=∠ADO
∵∠AOD= ![]() =
= ![]() ,∠ADO=
,∠ADO= ![]()
∴![]() =
= ![]()
∴![]()
②要使OA=OD,需∠OAD=∠ADO
∵∠OAD=![]() (∠AOD+∠ADO)=
(∠AOD+∠ADO)=![]() =
=![]()
∴![]() =
=![]()
∴![]()
③要使DO=DA,需∠OAD=∠AOD.
∵∠AOD= ![]() =
= ![]() ,∠OAD=
,∠OAD=![]() ∴
∴![]() =
=![]() ,解得
,解得![]()
综上所述:当![]() 的度数为
的度数为![]() 或
或或
![]() 时,△AOD是等腰三角形.
时,△AOD是等腰三角形.
“点睛”本题以“空间与图形”中的核心知识(如等边三角形)的性质、全等三角形的性质与证明、直角三角形的判定、多边形内角和等)为载体,内容由浅入深,层层递进,试题中几何演绎推理的难度适中,蕴含着丰富的思想方法(如运动变化、数形结合、分类讨论、方程思想等)能较好地考查学生的推理、探究及解决问题的能力.


 走进文言文系列答案
走进文言文系列答案科目:初中数学 来源: 题型:
【题目】四边形ABCD内部有1000个点,以顶点A、B、C、D、和这1000个点能把原四边形分割成n个 没有重叠的小三角形,则个数n的值为( )
A. 2002 B. 2001 C. 2000 D. 1001
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若当x=1时,代数式ax3+bx+7的值为-4,则当x=-1时,代数式ax3+bx+7值为( )
A. -4 B. 4 C. 10 D. 18
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若抛物线![]() 与
与![]() 满足
满足![]() ,则称
,则称![]() 互为“相关抛物线”给出如下结论:
互为“相关抛物线”给出如下结论:
①y1与y2的开口方向,开口大小不一定相同; ②y1与y2的对称轴相同;③若y2的最值为m,则y1的最值为k2m;④若函数![]() 与x 轴的两交点间距离为d,则函数
与x 轴的两交点间距离为d,则函数![]() 与x 轴的两交点间距离也为
与x 轴的两交点间距离也为![]() .其中正确的结论的序号是___________(把所有正确结论的序号都填在横线上).
.其中正确的结论的序号是___________(把所有正确结论的序号都填在横线上).
查看答案和解析>>
科目:初中数学 来源: 题型:
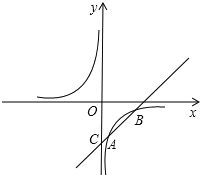
【题目】如图,已知反比例函数y =![]() 的图象经过点A(1,-3),一次函数y =kx +b的图象经过点A与点C(0,-4),且与反比例函数的图象相交于另一点B.试确定点B的坐标.
的图象经过点A(1,-3),一次函数y =kx +b的图象经过点A与点C(0,-4),且与反比例函数的图象相交于另一点B.试确定点B的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为推行公立医院改革,某医院将某药品经过两次降价,每瓶零售价由168元降为128元.已知两次降价的百分率相同,每次降价的百分率为x,根据题意列方程得( )
A. 168(1+x)2=128 B. 168(1-x)2=128 C. 168(1-2x)=128 D. 168(1-x2)=128
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列不等式中,正确的是( )
A.m与4的差是负数,可表示为m﹣4<0
B.x不大于3可表示为x<3
C.a是负数可表示为a>0
D.x与2的和是非负数可表示为x+2>0
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com