分析:连接BC1和AB1分别找其中点F,E,连接C2F与A2E并延长相交于Q点,根据三角形的中位线定理可得A2E=FB2,EB2=FC2,然后证明得到∠B2FC2=∠A2EB2,然后利用边角边定理证明得到△B2FC2与△A2EB2全等,根据全等三角形对应边相等可得A2B2=B2C2,再根据角的关系推出得到∠A2B2 C2=90°,从而得到A2B2与B2C2垂直且相等,同理可得其它边也垂直且相等,所以四边形A2B2C2D2是正方形.
解答: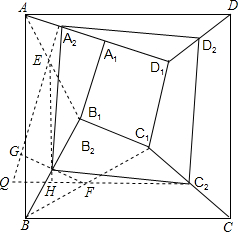
证明:如图,连接BC
1和AB
1分别找其中点F,E.连接C
2F与A
2E并延长相交于Q点,
连接EB
2并延长交C
2Q于H点,连接FB
2并延长交A
2Q于G点,
由A
2E=
A
1B
1=
B
1C
1=FB
2,EB
2=
AB=
BC=FC
2,
∵∠GFQ+∠Q=90°和∠GEB
2+∠Q=90°,
∴所以∠GEB
2=∠GFQ,
∴∠B
2FC
2=∠A
2EB
2,
可得△B
2FC
2≌△A
2EB
2,
所以A
2B
2=B
2C
2,
又∠HB
2C
2+∠HC
2B
2=90°和∠B
2C
2Q=∠EB
2A
2,
从而可得∠A
2B
2 C
2=90°,
同理可得其它边垂直且相等,
从而得出四边形A
2B
2C
2D
2是正方形.
点评:本题主要考查了正方形的性质与判定,三角形中位线定理,全等三角形的判定与性质,综合性较强,作辅助线构造出全等三角形是解题的关键.

 如图,已知四边形ABCD、A1B1C1D1都是正方形,A2、B2、C2、D2分别是AA1、BB1、CC1、DD1的中点.
如图,已知四边形ABCD、A1B1C1D1都是正方形,A2、B2、C2、D2分别是AA1、BB1、CC1、DD1的中点. 证明:如图,连接BC1和AB1分别找其中点F,E.连接C2F与A2E并延长相交于Q点,
证明:如图,连接BC1和AB1分别找其中点F,E.连接C2F与A2E并延长相交于Q点,

 新思维假期作业寒假吉林大学出版社系列答案
新思维假期作业寒假吉林大学出版社系列答案
 的延长线分别交于点F、E,且
的延长线分别交于点F、E,且
