
分析 (1)首先提取公因式(x+2)得到(x+2)(x-3)=0,然后解两个一元一次方程即可;
(2)把tan30°=$\frac{\sqrt{3}}{3}$、cos30°=$\frac{\sqrt{3}}{2}$和sin45°=$\frac{\sqrt{2}}{2}$代入原式进行化简求值即可.
解答 解:(1)解方程(x-1)(x+2)=2(x+2),
(x-1)(x+2)-2(x+2)=0,
(x+2)(x-1-2)=0,
(x+2)(x-3)=0,
x1=-2,x2=3;
(2)6tan30°-$\sqrt{3}$cos 30°-2sin 45°
=6×$\frac{\sqrt{3}}{3}$-$\sqrt{3}$×$\frac{\sqrt{3}}{2}$-2×$\frac{\sqrt{2}}{2}$
=2$\sqrt{3}$-$\frac{3}{2}$-$\sqrt{2}$.
点评 本题主要考查了因式分解法解一元二次方程以及特殊角的三角函数值等知识,解答本题的关键是掌握因式分解法解方程的方法与步骤以及熟记特殊角的三角函数值,此题难度不大.


 直通贵州名校周测月考直通名校系列答案
直通贵州名校周测月考直通名校系列答案 培优三好生系列答案
培优三好生系列答案科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:选择题
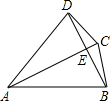 如图,AC平分∠DAB,AD=AC=AB,如下四个结论:①AC⊥BD;②BC=DE;③∠DBC=$\frac{1}{2}$∠DAC;④△ABC是正三角形,正确的结论有( )
如图,AC平分∠DAB,AD=AC=AB,如下四个结论:①AC⊥BD;②BC=DE;③∠DBC=$\frac{1}{2}$∠DAC;④△ABC是正三角形,正确的结论有( )| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | m2-4m-1 | B. | x2-2x-1 | C. | x2+2x+$\frac{1}{4}$ | D. | $\frac{1}{4}$b2-ab+a2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com