
分析 根据勾股定理的逆定理列出方程解即可,有第三边是斜边或者是直角边两种情况.
解答 解:根据勾股定理的逆定理列出方程解即可,有第三边是斜边或者是直角边两种情况.
当第三边是斜边时,第三边=$\sqrt{(\sqrt{2})^{2}+(\sqrt{3})^{2}}$=$\sqrt{2+3}$=$\sqrt{5}$(cm);
当第三边是直角边时,第三边=$\sqrt{(\sqrt{3})^{2}-(\sqrt{2})^{2}}$=1(cm).
综上所述,第三条线段的长是$\sqrt{5}$cm或1cm.
故答案为:$\sqrt{5}$cm或1cm.
点评 本题考查的是勾股定理,熟知在任何一个直角三角形中,两条直角边长的平方之和一定等于斜边长的平方是解答此题的关键.


科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:选择题
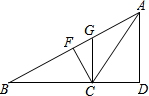 如图,AD⊥BC于点D,GC⊥BC于点C,CF⊥AB于点F,下列关于高的说法中错误的是( )
如图,AD⊥BC于点D,GC⊥BC于点C,CF⊥AB于点F,下列关于高的说法中错误的是( )| A. | △ABC中,AD是BC边上的高 | B. | △GBC中,CF是BG边上的高 | ||
| C. | △ABC中,GC是BC边上的高 | D. | △GBC中,GC是BC边上的高 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
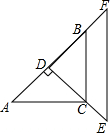 已知:有两块完全相同的含45°角的三角板,如图,将Rt△DEF的直角的顶点D放在Rt△ABC斜边AB的中点处,这时两块三角板重叠部分△DBC的面积是△ABC的面积的$\frac{1}{2}$.
已知:有两块完全相同的含45°角的三角板,如图,将Rt△DEF的直角的顶点D放在Rt△ABC斜边AB的中点处,这时两块三角板重叠部分△DBC的面积是△ABC的面积的$\frac{1}{2}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com