


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:

查看答案和解析>>
科目:初中数学 来源: 题型:
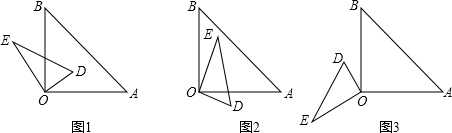
 如图,将两个全等的等腰直角三角形摆成如图所示的样子(顶点A重合),
如图,将两个全等的等腰直角三角形摆成如图所示的样子(顶点A重合),查看答案和解析>>
科目:初中数学 来源: 题型:
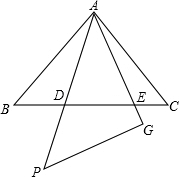
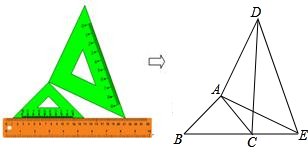 将两个大小不同的含45°角的直角三角板如图1所示放置在同一平面内.从图1中抽象出一个几何图形(如图2),B、C、E三点在同一条直线上,连接DC.
将两个大小不同的含45°角的直角三角板如图1所示放置在同一平面内.从图1中抽象出一个几何图形(如图2),B、C、E三点在同一条直线上,连接DC.查看答案和解析>>
科目:初中数学 来源: 题型:

查看答案和解析>>
科目:初中数学 来源: 题型:
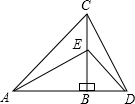 如图,将两个一大、一小的等腰直角三角尺拼接 (A、B、D三点共线,AB=CB,EB=DB,∠ABC=∠EBD=90°),连接AE、CD,试确定AE与CD的位置与数量关系,并证明你的结论.
如图,将两个一大、一小的等腰直角三角尺拼接 (A、B、D三点共线,AB=CB,EB=DB,∠ABC=∠EBD=90°),连接AE、CD,试确定AE与CD的位置与数量关系,并证明你的结论.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com