
| 5 |
| 2 |
| 13 |
| 2 |
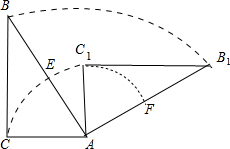 以点A为圆心,AC为半径的弧交AB于E,交AB1于F,如图,
以点A为圆心,AC为半径的弧交AB于E,交AB1于F,如图,| 90•π•5 |
| 180 |
| 5 |
| 2 |
| 90•π•13 |
| 180 |
| 13 |
| 2 |
| 13 |
| 2 |
| 5 |
| 2 |
| 90•π•132 |
| 360 |
| 90•π•52 |
| 360 |


科目:初中数学 来源: 题型:
 如图是6×8的正方形网格,△ABC的顶点都在格点上,M、N也在格点上.
如图是6×8的正方形网格,△ABC的顶点都在格点上,M、N也在格点上.查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
| x | -3 | -2 | -1 | 0 | 1 | 2 | 3 |
| y1 | |||||||
| y2 |
查看答案和解析>>
科目:初中数学 来源: 题型:
 已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,有下列结论:①abc>0;②a+b+c=0;③a>
已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,有下列结论:①abc>0;②a+b+c=0;③a>| 1 |
| 2 |
| A、①② | B、②③ | C、②④ | D、③④ |
查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
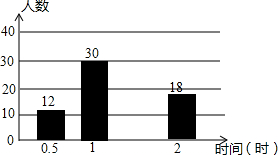 在济南市开展的“美丽泉城,创卫我同行”活动中,某校倡议七年级学生利用双休日在各自社区参加义务劳动.为了解同学们劳动情况,学校随机调查了部分同学的劳动时间,并用得到的数据绘制成不完整的统计图表,如图所示:
在济南市开展的“美丽泉城,创卫我同行”活动中,某校倡议七年级学生利用双休日在各自社区参加义务劳动.为了解同学们劳动情况,学校随机调查了部分同学的劳动时间,并用得到的数据绘制成不完整的统计图表,如图所示:| 劳动时间(时) | 频数(人数) | 频率 |
| 0.5 | 12 | 0.12 |
| 1 | 30 | 0.3 |
| 1.5 | x | 0.4 |
| 2 | 18 | y |
| 合计 | m | 1 |
查看答案和解析>>
科目:初中数学 来源: 题型:
| A、36,38 |
| B、37,38 |
| C、36.5,38 |
| D、37,36.5 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com