
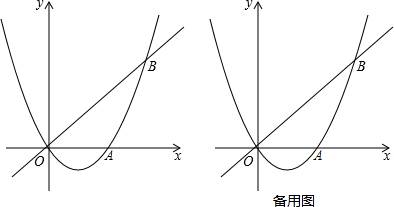
分析 (1)把y=$\frac{3}{4}$代入直线解析式,即可求得B的坐标,然后把A和B的坐标代入二次函数解析式求解;
(2)设P的坐标是(t,t2-$\frac{5}{4}t$),则D的坐标是(t,$\frac{3}{4}t$),在直角△OCD和直角△PHD中根据三角函数的关系得到PH和PD的关系,从而列方程求解;
(3)过点P作PC⊥x轴于点C,连接OP,证明直角△OHP≌直角△OCP,根据PH=PC即可列方程求解.
解答 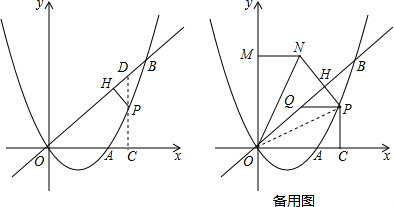 解:(1)把y=$\frac{3}{4}$代入y=$\frac{3}{4}x$中,$\frac{3}{4}x=\frac{3}{2}$,解得:x=2,
解:(1)把y=$\frac{3}{4}$代入y=$\frac{3}{4}x$中,$\frac{3}{4}x=\frac{3}{2}$,解得:x=2,
则B的坐标是(2,$\frac{3}{2}$).
把A($\frac{5}{4}$,0),B(2,$\frac{3}{2}$)代入y=ax2+bx,得$\left\{\begin{array}{l}{(\frac{5}{4})^{2}a+\frac{5}{4}b=0}\\{4a+2b=\frac{3}{2}}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{a=1}\\{b=-\frac{5}{4}}\end{array}\right.$,
则a=1,b=-$\frac{5}{4}$;
(2)过点P作x轴的垂线,交x轴于点C,交OB于点D,
∵P的横坐标是t,抛物线解析式是y=x2-$\frac{5}{4}x$,
∴P的坐标是(t,t2-$\frac{5}{4}t$),D的坐标是(t,$\frac{3}{4}t$).
∴PD=$\frac{3}{4}t-({t}^{2}-\frac{5}{4}t)$=-t2+2t,
CD=$\frac{3}{4}t$,OC=t,
∴OD=$\sqrt{O{C}^{2}+C{D}^{2}}$=$\frac{5}{4}t$,
∴在直角△OCD中,sin∠ODC=$\frac{OC}{OD}$=$\frac{4}{5}$,在直角△PHD中,sin∠ODC=$\frac{PH}{PD}$=$\frac{4}{5}$,
∴PH=$\frac{4}{5}PD$,
∴PH=$\frac{4}{5}$(-t2+2t)=-$\frac{4}{5}{t}^{2}+\frac{8}{5}t$,
∴d=-$\frac{4}{5}{t}^{2}+\frac{8}{5}t$;
(3)过点P作PC⊥x轴于点C,连接OP,
∵MN∥x轴,PQ∥x轴,
∴MN∥PQ.
∴∠MNP+∠HPQ=180°,
∵MN∥x轴,
∴∠OMN=90°,
∴∠ONM+∠MON=90°,
又∵∠ONM+HPQ-∠MON=90°,
∴2∠ONM=180°-∠HPQ=∠MNP,
∴∠ONM=∠ONP,OM⊥MN,OH⊥PN,M的坐标是 (0,t),
∴OM=OH=t,
∵P的横坐标是t,
∴OC=t,
∴OC=OH.
∴在直角△OHP和直角△OCP中,
$\left\{\begin{array}{l}{OC=OH}\\{OP=OP}\end{array}\right.$,
∴直角△OHP≌直角△OCP,
∴PH=PC,
由(2)知PH=-$\frac{4}{5}$t2+$\frac{8}{5}$t,PC=t2-$\frac{5}{4}$t,
∴-$\frac{4}{5}$t2+$\frac{8}{5}$t=t2-$\frac{5}{4}$t,
解得:t=0(舍去),t=$\frac{19}{12}$.
∴此时t的值是$\frac{19}{12}$.
点评 本题着重考查了待定系数法求二次函数解析式,以及全等三角形的判定和性质、三角函数,正确作出辅助线,证明直角△OHP≌直角△OCP,转化为方程问题是关键.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:选择题
| A. | 篮球队员在罚球线上投篮一次,未投中是必然事件 | |
| B. | 想了解某种饮料中含色素的情况,宜采用普查 | |
| C. | 数据5,1,-2,2,3的中位数是-2 | |
| D. | 一组数据的波动越大,方差越大 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
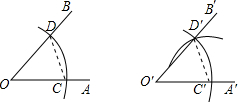 请仔细观察用直尺和圆规作一个角∠A′O′B′等于已知角∠AOB的示意图,要说明∠D′O′C′=∠DOC,需要证明△D′O′C′≌△DOC,则这两个三角形全等的依据是( )
请仔细观察用直尺和圆规作一个角∠A′O′B′等于已知角∠AOB的示意图,要说明∠D′O′C′=∠DOC,需要证明△D′O′C′≌△DOC,则这两个三角形全等的依据是( )| A. | 边边边 | B. | 边角边 | C. | 角边角 | D. | 角角边 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
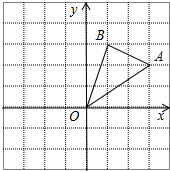 如图,在边长为1的正方形组成的网格中,△AOB的顶点均在格点上,点A、B的坐标分别是A(3,2)、B(1,3).△AOB绕点O逆时针旋转90°后得到△A1OB1.
如图,在边长为1的正方形组成的网格中,△AOB的顶点均在格点上,点A、B的坐标分别是A(3,2)、B(1,3).△AOB绕点O逆时针旋转90°后得到△A1OB1.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,直线y=-x+m与y=x+3的交点的横坐标为-2,则关于x的不等式-x+m>x+3>0的取值范围为( )
如图,直线y=-x+m与y=x+3的交点的横坐标为-2,则关于x的不等式-x+m>x+3>0的取值范围为( )| A. | x>-2 | B. | x<-2 | C. | -3<x<-2 | D. | -3<x<-1 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
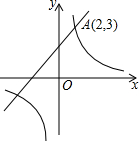 如图,一次函数y1=k1x+b(k1、b为常数,且k1≠0)的图象与反比例函数y2=$\frac{{k}_{2}}{x}$(k2为常数,且k2≠0)的图象都经过点A(2,3).则当x>2时,y1与y2的大小关系为y1>y2.
如图,一次函数y1=k1x+b(k1、b为常数,且k1≠0)的图象与反比例函数y2=$\frac{{k}_{2}}{x}$(k2为常数,且k2≠0)的图象都经过点A(2,3).则当x>2时,y1与y2的大小关系为y1>y2.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,AD、BC是⊙O的两条互相垂直的直径,点P从点O出发,沿O→C→D→O的路线匀速运动.设∠APB=y(单位:度),那么y关于点P运动的时间x(单位:秒)的函数图象大致是( )
如图,AD、BC是⊙O的两条互相垂直的直径,点P从点O出发,沿O→C→D→O的路线匀速运动.设∠APB=y(单位:度),那么y关于点P运动的时间x(单位:秒)的函数图象大致是( )| A. |  | B. | 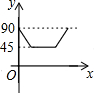 | C. |  | D. |  |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:填空题
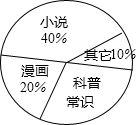 为了解学生课外阅读的喜好,某校从八年级1200名学生中随机抽取50名学生进行问卷调查,整理数据后绘制如图所示的统计图.由此可估计该年级喜爱“科普常识”的学生约有360人.
为了解学生课外阅读的喜好,某校从八年级1200名学生中随机抽取50名学生进行问卷调查,整理数据后绘制如图所示的统计图.由此可估计该年级喜爱“科普常识”的学生约有360人.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com