
����Ŀ������������8�֣�����ʵ����ѧ����ҵ��������������ҵ�ĸ��һ����Ҫ�ٴ룮ij��ѧΪ�˽ⱾУѧ��ƽ��ÿ��Ŀ�����ҵʱ�䣬�����ȡ����ѧ�������ʾ����飬������������ΪA��B��C��D�ĸ��ȼ���A��1Сʱ���ڣ�B��1Сʱ-1��5Сʱ��C��1��5Сʱ-2Сʱ��D��Сʱ���ϣ����ݵ�������������ͼ��ʾ��������������ͳ��ͼ�������ͼ����Ϣ����������⣺
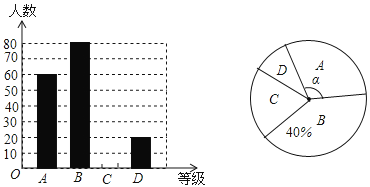
��1����У��������_________��ѧ����
��2���뽫����ͳ��ͼ����������
��3����ʾ�ȼ�A������Բ�Ľ�![]() �Ķ�����____________��
�Ķ�����____________��
��4���ڴ˴��ʾ������У��ס����������2��ƽ��ÿ�������ҵʱ�䶼��2Сʱ���ϣ�����4������ѡ2��ȥ�μ���̸�����б�����״ͼ�ķ�����ѡ����2�����Բ�ͬ�༶�ĸ��ʣ�
���𰸡���1��200�ˣ���2������������3��![]() ����4��
����4��![]() ��
��
��������
���⣨1��������ͼ�����ǿ��Կ��ó�A������Ϊ60��B������Ϊ80��D������Ϊ20��������ͳ��ͼ�������ܿ���Bռ�ı���40%���������Ǻ������ܵó���������200�ˣ�
��2���������ܵó�C������40�ˣ�ͼ�ο������в��䣩��
��3��Aռ�ı��ؼ�����Բ�Ľ�![]() �Ķ���Ϊ��
�Ķ���Ϊ��![]() =
=![]() ��
��
���������ѧ�����Ƿֱ��ʾΪ��A����B����A����B����һ����![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ���������Ǿͺ����ó��������Բ�ͬ�༶�ĸ���Ϊ��
���������Ǿͺ����ó��������Բ�ͬ�༶�ĸ���Ϊ��![]()
�����������1���⣺��1��200����2����ͼ���£�

��2���⣺60��200=30%��
��3���⣺��װ�ѧ��Ϊ![]() ��
��![]() �������п��ܵ����Ϊ��
�������п��ܵ����Ϊ��![]() ������
������![]() ����
����
��![]() ����
����![]() ����
����![]() ��
��![]() ������������Բ���ͬһ�����������֣�����Ϊ
������������Բ���ͬһ�����������֣�����Ϊ![]() ��
��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���Ķ�������ϣ�
����ѧ���ϣ���ʦ������ó߹���ͼ����������⣺
��֪����ACB�ǡ�ABC��һ���ڽǣ�
��������APB=��ACB��
С�����������£�
��ͼ
�����߶�AB�Ĵ�ֱƽ����m��
�����߶�BC�Ĵ�ֱƽ����n����ֱ��m���ڵ�O��
���Ե�OΪԲ�ģ�OAΪ�뾶����ABC�����Բ��
���ڻ�ACB��ȡһ��P������AP��BP��
���ԡ�APB=��ACB��
��ʦ˵����С����������ȷ����
��ش�
��1����OΪ��ABC���ԲԲ�ģ���OA=OB=OC����������_____��
��2����APB=��ACB��������_____��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����ͼ������������y= ![]() ��ͼ����һ�κ���y=x+b��ͼ��
��ͼ����һ�κ���y=x+b��ͼ��
�ڵ�A��1��4������B��-4��n����

��1����һ�κ����ͷ����������Ľ���ʽ��
��2�����OAB�������
��3��ֱ��д��һ�κ���ֵ���ڷ���������ֵ���Ա���x��ȡֵ��Χ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
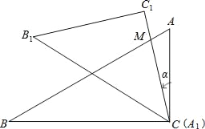
����Ŀ����ͼ����һ��ѧ���õ����ǰ壬����ABC �У���C��90������A��60������B��30��������A1B1C1�У���C1��90������B1A1 C1��45������B1��45������A1B1��CB��������A1C1���CA�غϣ����е�A1���C�غϣ������ǰ�A1B1C1�Ƶ�C��A1������ʱ�뷽����ת����ת���Ľ�Ϊ������ת�����б�A1C1���AB�Ľ���ΪM����AC��a��
��1������A1C1�ij���
��2��������30��ʱ��֤����B1C1��AB��
��3����a��![]() ��������45��ʱ�������������ǰ��ص�����ͼ�ε������
��������45��ʱ�������������ǰ��ص�����ͼ�ε������
��4��������60��ʱ���ú�a�Ĵ���ʽ��ʾ�������ǰ��ص�����ͼ�ε������
���ο����ݣ�sin15����![]() ��cos15����
��cos15����![]() ��tan15����2��
��tan15����2��![]() ��sin75����
��sin75����![]() ��cos75����
��cos75����![]() ��tan75����2+
��tan75����2+![]() ��
��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ı���ABCD���ĸ�����ֱ��ڷ���������![]() ��
��![]() (x��0��0��m��n)��ͼ���ϣ��Խ���BD//y�ᣬ��BD��AC�ڵ�P����֪��B�ĺ�����Ϊ4��
(x��0��0��m��n)��ͼ���ϣ��Խ���BD//y�ᣬ��BD��AC�ڵ�P����֪��B�ĺ�����Ϊ4��
��1����m=4��n=20ʱ��
������P��������Ϊ2����ֱ��AB�ĺ�������ʽ��
������P��BD���е㣬���ж��ı���ABCD����״����˵�����ɣ�
��2���ı���ABCD�ܷ��Ϊ�����Σ����ܣ����ʱm��n֮���������ϵ�������ܣ���˵�����ɣ�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪������y=![]() x2+bx+c������ABC���������㣬���е�A��0��1������B����9��10����AC��x�ᣬ��Pʱֱ��AC�·��������ϵĶ��㣮
x2+bx+c������ABC���������㣬���е�A��0��1������B����9��10����AC��x�ᣬ��Pʱֱ��AC�·��������ϵĶ��㣮

��1���������ߵĽ���ʽ����2������P����y��ƽ�е�ֱ��l��ֱ��AB��AC�ֱ��ڵ�E��F�����ı���AECP��������ʱ�����P�����ꣻ
��3������PΪ�����ߵĶ���ʱ����ֱ��AC���Ƿ���ڵ�Q��ʹ����C��P��QΪ��������������ABC���ƣ������ڣ������Q�����꣬�������ڣ���˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
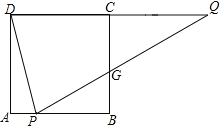
����Ŀ����ͼ���ڱ߳�Ϊ2��������ABCD�У���P��AB�ϣ���Q��DC���ӳ����ϣ�����DP��QP���ҡ�APD=��QPD��PQ��BC�ڵ�G��
��1����֤��DQ=PQ��
��2����tan��APD=![]() ʱ����CQ�ij�����BG�ij���
ʱ����CQ�ij�����BG�ij���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
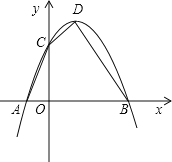
����Ŀ����֪����ͼ��������y=ax2-2ax+c��a��0����y�ύ�ڵ�C��0��3������x�ύ��A��B���㣬��A������Ϊ��-1��0����
��1���������ߵĽ���ʽ������D�����ꣻ
��2�����P���ڵ�һ�������������ϵ�һ�����㣬��ʹ���ı���ACDB�����ȵ��ı���ACPB�ĵ�P�����ꣻ
��3������APD�������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�������Ĵ�����װ��4����ͬ��С�����dz���ɫ����������𣬰����Ƿֱ��ţ�1��2��3��4��
��1���������һ��С��Żز�ҡ�ȣ����������һ�������б�����״ͼ�ķ������������ȡ��������ͬ���ĸ���
��2�������������С��ֱ��д��������ȡ�������ź͵���4���ĸ��ʣ�
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com