
【题目】已知:如图,抛物线y=ax2-2ax+c(a≠0)与y轴交于点C(0,3),与x轴交于A、B两点,点A的坐标为(-1,0).
(1)求抛物线的解析式及顶点D的坐标;
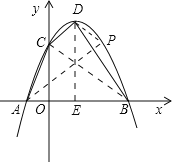
(2)设点P是在第一象限内抛物线上的一个动点,求使与四边形ACDB面积相等的四边形ACPB的点P的坐标;
(3)求△APD的面积.
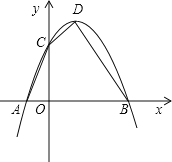
【答案】(1)y=-x2+2x+3,(1,4);(2)点P的坐标是(2,3);(3)△APD的面积是3.
【解析】
(1)根据抛物线y=ax2-2ax+c(a≠0)与y轴交于点C(0,3),与x轴交于A(-1,0),代入即可求出a、c的值,即得到解析式,化成顶点式就能求出顶点坐标;
(2)连接BC,过点D作DE⊥x轴于点E,令y=0,求出B的坐标,根据点的坐标和面积公式能求出四边形ACDB和△BCD的面积,根据B、C的坐标能求出直线BC,设直线DP的函数解析式为y=-x+b,把点D(1,4)代入即可求出直线DP的函数解析式,求出y=-x+5和y=-x2+2x+3组成的方程组的解即可;
(3)根据对称得到△APD≌△BCD,根据全等三角形的性质即可得到答案.
(1)∵抛物线y=ax2-2ax+c(a≠0)与y轴交于点C(0,3),与x轴
交于A(-1,0)
∴
![]() ,
,
解得
![]() ,
,
∴抛物线的解析式为y=-x2+2x+3,
∵y=-(x2-2x)+3=-(x2-2x+1-1)+3=-(x-1)2+4,
∴顶点D的坐标为(1,4),
答:抛物线的解析式是y=-x2+2x+3,顶点D的坐标是(1,4).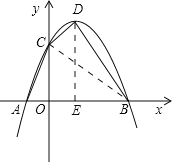
(2)连接BC,过点D作DE⊥x轴于点E.
令y=0则-x2+2x+3=0,
∴x1=-1,x2=3
∴点B的坐标为(3,0),
∴S四边形ACDB=S△AOC+S梯形OEDC+S△EBD=![]() ×1×3+
×1×3+![]() ×(3+4)×1+
×(3+4)×1+![]() ×2×4=9
×2×4=9
∵S△ABC=![]() ×4×3=6
×4×3=6
∴S△BCD=3
∵点P是在第一象限内抛物线上的一个动点,S四边形ACDB=S四边形ACPB,
∴S△BCP=S△BCD=3,
∴点P是过D且与直线BC平行的直线和抛物线的交点,
而直线BC的函数解析式为y=-x+3,
∴设直线DP的函数解析式为y=-x+b,过点D(1,4),
∴-1+b=4,b=5,
∴直线DP的函数解析式为y=-x+5,
把y=-x+5代入y=-x2+2x+3中,解得x1=1,x2=2,
∴点P的坐标为(2,3),
答:与四边形ACDB面积相等的四边形ACPB的点P的坐标是(2,3).
(3)∵点P与点C关于DE对称,点B与点A关于DE对称,
∴△APD≌△BCD,
∴S△APD=S△BCD=3,
答:△APD的面积是3.


科目:初中数学 来源: 题型:
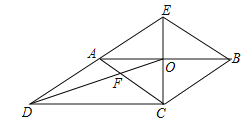
【题目】如图,CE是ABCD的边AB的垂直平分线,垂足为点O,CE与DA的延长线交于点E.连接AC,BE,DO,DO与AC交于点F,则下列结论:
①四边形ACBE是菱形;
②∠ACD=∠BAE;
③AF:BE=2:3;
④S四边形AFOE:S△COD=2:3.
其中正确的结论有_____.(填写所有正确结论的序号)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(本题满分8分)“切实减轻学生课业负担”是我市作业改革的一项重要举措.某中学为了解本校学生平均每天的课外作业时间,随机抽取部分学生进行问卷调查,并将调查结果分为A、B、C、D四个等级.A:1小时以内,B:1小时-1.5小时,C:1.5小时-2小时,D:小时以上.根据调查结果绘制了如图所示的两幅不完整的统计图.请根据图中信息解答下列问题:
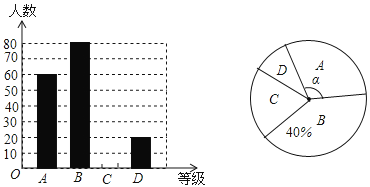
(1)该校共调查了_________名学生;
(2)请将条形统计图补充完整;
(3)表示等级A的扇形圆心角![]() 的度数是____________;
的度数是____________;
(4)在此次问卷调查中,甲、乙两班各有2人平均每天课外作业时间都是2小时以上,从这4人中任选2人去参加座谈,用列表或树状图的方法求选出的2人来自不同班级的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在![]() 中,
中,![]() ,
,![]() 平分
平分![]() 交
交![]() 于点
于点![]() ,
,![]() 为
为![]() 上一点,经过点
上一点,经过点![]() ,
,![]() 的
的![]() 分别交
分别交![]() ,
,![]() 于点
于点![]() ,
,![]() ,连接
,连接![]() 交
交![]() 于点
于点![]() .
.
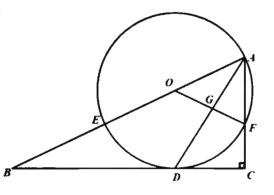
(1)求证:![]() 是
是![]() 的切线;
的切线;
(2)设![]() ,
,![]() ,试用含
,试用含![]() 的代数式表示线段
的代数式表示线段![]() 的长;
的长;
(3)若![]() ,
,![]() ,求
,求![]() 的长.
的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一中在每年5月都会举行艺术节活动,活动的形式有A.唱歌、B.跳舞、C.绘画、D.演讲四种形式,学校围绕“你最喜欢的活动方式是什么?”在八年级学生中进行随机抽样调查(四个选项中必须且只选一项),根据调查统计结果,绘制了如图两种不完整的统计图表: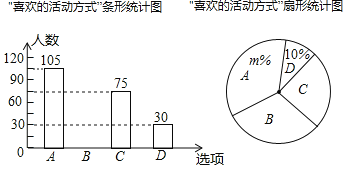
请结合统计图表,回答下列问题:
(1)本次抽查的学生共300人,m=35,并将条形统计图补充完整;
(2)学校采用抽签方式让每班在A、B、C、D四项进行展示,请用树状图或列表法求某班所抽到的两项方式恰好是“唱歌”和“舞蹈”的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
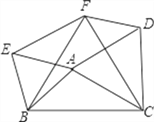
【题目】如图,以△ABC的三边为边分别作等边△ACD、△ABE、△BCF。
(1)求证:△EBF≌△DFC;
(2)求证:四边形AEFD是平行四边形;
(3)①△ABC满足_____________________时,四边形AEFD是菱形。(无需证明)
②△ABC满足_______________________时,四边形AEFD是矩形。(无需证明)
③△ABC满足_______________________时,四边形AEFD是正方形。(无需证明)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为满足市场需求,某超市在八月十五“中秋节”来临前夕,购进一种品牌的月饼,每盒进价40元,根据以往的销售经验发现:当售价定为每盒45元时,每天可以卖出700盒,每盒售价每提高1元,每天要少卖出20盒.
![]() 写出每天的销售量
写出每天的销售量![]() 盒
盒![]() 与每盒月饼上涨
与每盒月饼上涨![]() 元
元![]() 之间的函数关系式.
之间的函数关系式.
![]() 当每盒售价定为多少元时,当天的销售利润
当每盒售价定为多少元时,当天的销售利润![]() 元
元![]() 最大?最大利润是多少?
最大?最大利润是多少?
![]() 为稳定物价,有关管理部门限定,这种月饼每盒的利润不得高于进价的
为稳定物价,有关管理部门限定,这种月饼每盒的利润不得高于进价的![]() ,那么超市每天获得最大利润是多少?
,那么超市每天获得最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,抛物线![]() 交x轴于A(-2,0),B(3,0)两点,交y轴于点C(0,6).
交x轴于A(-2,0),B(3,0)两点,交y轴于点C(0,6).
(1)写出a,b,c的值;
(2)连接BC,点P为第一象限抛物线上一点,过点A作AD⊥x轴,过点P作PD⊥BC于交直线AD于点D,设点P的横坐标为t,AD长为h.
①求h与t的函数关系式和h的最大值(请求出自变量t的取值范围);
②过第二象限点D作DE∥AB交BC于点E,若DP=CE,时,求点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
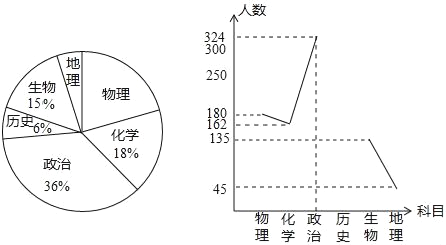
【题目】某校对九年级学生进行随机抽样调查,被抽到的学生从物理、化学、生物、地理、历史和政治这六科中选出自己最喜欢的科目,将调查数据汇总整理后,绘制了两幅不同的统计图,请你根据图中信息解答下列问题:
(1)被抽查的学生共有多少人?求出地理学科所在扇形的圆心角;
(2)将折线统计图补充完整;
(3)若该校九年级学生约2000人请你估算喜欢物理学科的人数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com