
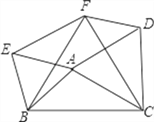
【题目】如图,以△ABC的三边为边分别作等边△ACD、△ABE、△BCF。
(1)求证:△EBF≌△DFC;
(2)求证:四边形AEFD是平行四边形;
(3)①△ABC满足_____________________时,四边形AEFD是菱形。(无需证明)
②△ABC满足_______________________时,四边形AEFD是矩形。(无需证明)
③△ABC满足_______________________时,四边形AEFD是正方形。(无需证明)
【答案】(1)证明见解析;
(2)证明见解析;
(3)①AB=AC②∠BAC=150°,③AB=AC,∠BAC=150°
【解析】试题分析:(1)由三角形BCF与三角形AEB为等边三角形,利用等边三角形的性质得到两对边相等,一对角相等,利用等式的性质得到夹角相等,利用SAS即可得证;
(2)可通过证△EFB≌△ACB,得EF=AC=AD;然后证△CDF≌△CAB,得DF=AB=AE;从而证得四边形ADFE的两组对边分别相等,即可得出ADFE是平行四边形;
(3)①当∠BAC=150°,由此可求得∠EAD的度数,则可得ADFE是矩形;
②当AE=AD时,ADFE是菱形;
③当ADFE是正方形时,∠EAD=90°,且AE=AD,联立(2)(3)的结论即可.
试题解析:(1)连接EF、DF,
∵△ABE、△CBF是等边三角形,
∴BE=AB,BF=CB,∠EBA=∠FBC=60°;
∴∠EBF=∠ABC=60°-∠ABF;
∴△EFB≌△ACB;
∴EF=AC=AD;
(2)同理由△CDF≌△CAB,得DF=AB=AE;
(3)①由AE=DF,AD=EF即可得出四边形AEFD是平行四边形;若∠BAC=150°,则平行四边形AEFD是矩形;
②由(2)知四边形AEFD是平行四边形,则∠EAD=90°时,可得平行四边形AEFD是矩形,∴∠BAC=360°-60°-60°-90°=150°,即△ABC满足∠BAC=150°时,四边形AEFD是矩形;
③综合①②的结论知:当△ABC是顶角∠BAC是150°的等腰三角形时,四边形AEFD是正方形.


科目:初中数学 来源: 题型:
【题目】已知二次函数y=2x2+bx﹣1.
(1)求证:无论b取什么值,二次函数y=2x2+bx﹣1图象与x轴必有两个交点.
(2)若两点P(﹣3,m)和Q(1,m)在该函数图象上.
①求b、m的值;
②将二次函数图象向上平移多少单位长度后,得到的函数图象与x轴只有一个公共点?
查看答案和解析>>
科目:初中数学 来源: 题型:
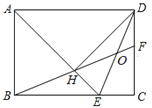
【题目】如图,在矩形ABCD中,AD=![]() AB,∠BAD的平分线交BC于点E,DH⊥AE于点H,连接BH并延长交CD于点F,连接DE交BF于点O,下列结论:
AB,∠BAD的平分线交BC于点E,DH⊥AE于点H,连接BH并延长交CD于点F,连接DE交BF于点O,下列结论:
①∠AED=∠CED;②OE=OD;③BH=HF;④BC-CF=2HE;⑤AB=HF,其中正确的有( )
A. ①②③④⑤ B. ①②③④ C. ①③④⑤ D. ①②③⑤
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明在利用完全平方公式计算一个二项整式的平方时,不小心用墨水把中间一项的系数染黑了,得到正确的结果为4a2■ab+9b2 , 你认为这个二项整式应是( )
A.2a+3b
B.2a﹣3b
C.2a±3b
D.4a±9b
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】用长为20cm的铁丝,折成一个矩形,设它的一边长为xcm,面积为ycm2.
(1)求出y与x的函数关系式。(不写自变量的取值范围)
(2)当边长x为多少时,矩形的面积最大,最大面积是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】规定两数a,b之间的一种运算,记作(a,b):如果![]()
![]() ,那么(a,b)=c.
,那么(a,b)=c.
例如:因为23=8,所以(2,8)=3.
(1)根据上述规定,填空:
(3,27)=_______,(5,1)=_______,(2,![]()
![]() )=_______.
)=_______.
(2)小明在研究这种运算时发现一个现象:(3n,4n)=(3,4)小明给出了如下的证明:
设(3n,4n)=x,则(3n)x=4n,即(3x)n=4n
所以3x=4,即(3,4)=x,
所以(3n,4n)=(3,4).
请你尝试运用这种方法证明下面这个等式:(3,4)+(3,5)=(3,20)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com